
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2x+\frac{\pi}{6}=\frac{\pi}{2}+k\pi\)
\(\Leftrightarrow2x=\frac{\pi}{3}+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{6}+\frac{k\pi}{2}\)

cau 12:
gọi E là trung điểm AB \(\Rightarrow\)MẸ//BC ; và EN// AC do do ME=BD/2 ;NE= AC/2
\(\Rightarrow\left[\widehat{BD;AC}\right]=\left[\widehat{ME;EN}\right]=90^0\)
\(\Delta MEN\)vuông tại E\(\Rightarrow MN^2=ME^2+NE^2=\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2=\left(\dfrac{10a^2}{4}\right)\Rightarrow MN=\dfrac{a\sqrt{10}}{2}\)
chọn đáp án A
vẽ hình ở ngoài rồi dán vào ko biết tại sao nó lại thụt xuống dưới![]()


Gọi \(\overline{abcde}\)là số cần tìm.
Vì \(\overline{abcde}\)là số chẵn nên \(e\in\left\{0;2;4;6;8\right\}\)
*Trường hợp 1: e=0
Có 2 cách chọn a(\(a\ne e\)và \(a\le2\))
Có 3 cách chọn b(\(b\ne a\ne e\)và b<5)
Có 4 cách chọn c
Có 3 cách chọn d
Áp dụng quy tắc nhân ta được:2.3.4.3.1=72 số
*Trường hợp 2: e=2
Có 1 cách chọn a
Có 3 cách chọn b
Có 4 cách chọn c
Có 3 cách chọn d
Áp dụng quy tắc nhân có 1.3.4.3.1=24 số
*Trường hợp 3:e=4
Có 2 cách chọn a
Có 3 cách chọn b
Có 4 cách chọn c
Có 3 cách chọn d
Áp dụng quy tắc nhân có: 2.3.4.3.1=72 số
*Trường hợp 4:\(e\in\left\{6;8\right\}\)
Có 2 cách chon a
Có 4 cách chọn b
Có 4 cách chọn c
Có 3 cách chọn d
Áp dụng quy tắc nhân có:2.4.4.3.2=192 số
Vậy số các số chẵn có 5 chữ số khác nhau và nhỏ hơn 25000 là:72+24+72+192=360 số

pt<=>-cos4x-sin4x=sinx-cosx
<=>-(sin4x+cos4x)=sinx-cosx
<=>-\(\sqrt{2}\)sin(4x+\(\dfrac{\Pi}{4}\))=\(\sqrt{2}\)sin(x-\(\dfrac{\Pi}{4}\))
<=>sin(-4x-\(\dfrac{\Pi}{4}\))=sin(x-\(\dfrac{\Pi}{4}\))
tới đây bạn tự giải nha!!
 làm hộ em bài 3Nhãn
làm hộ em bài 3Nhãn
 Ai giải chi tiết cái này hộ mình với
Ai giải chi tiết cái này hộ mình với
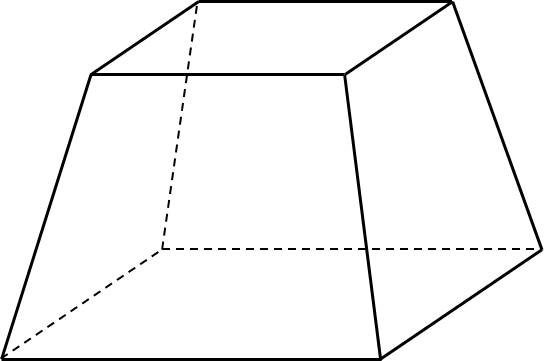
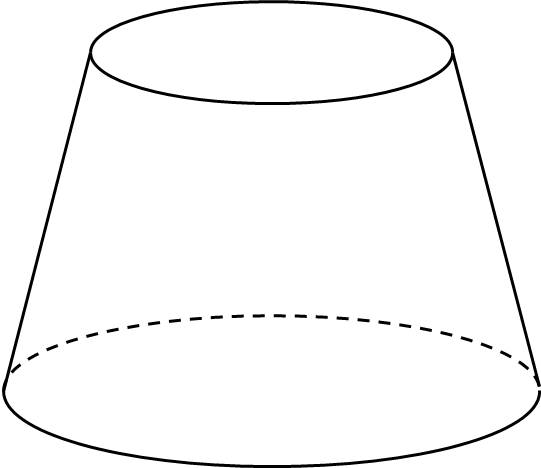
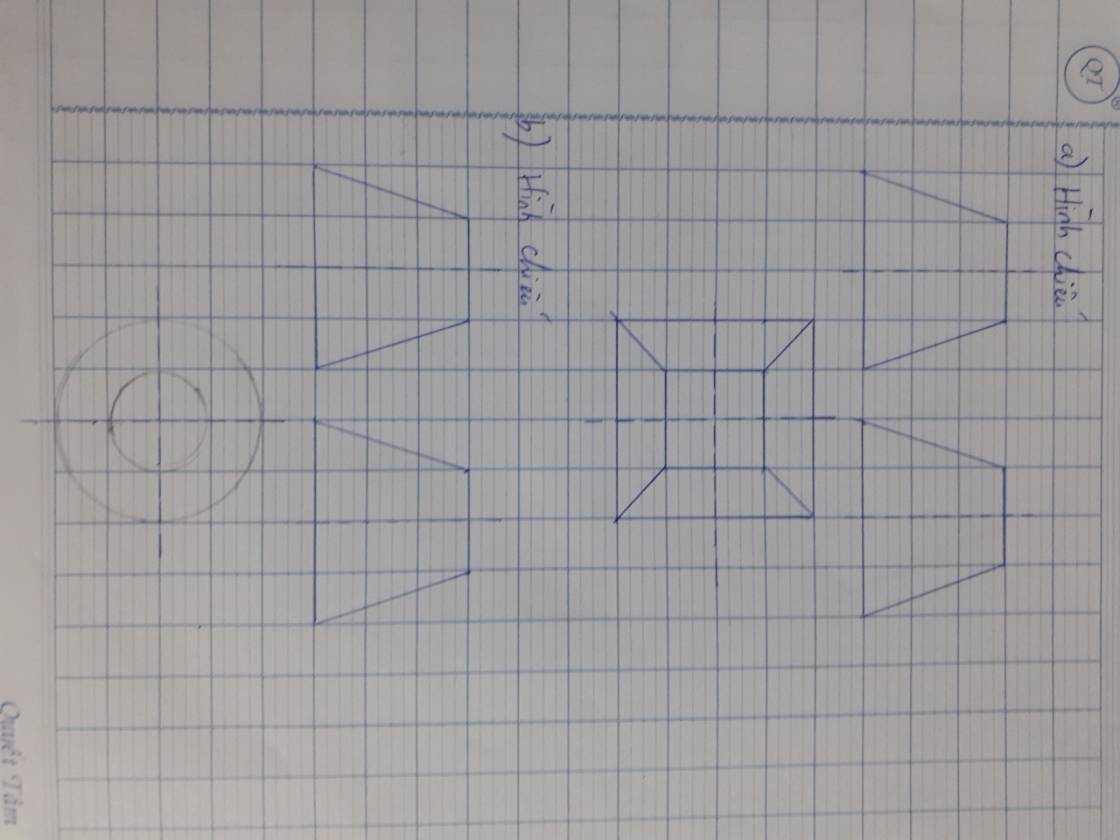
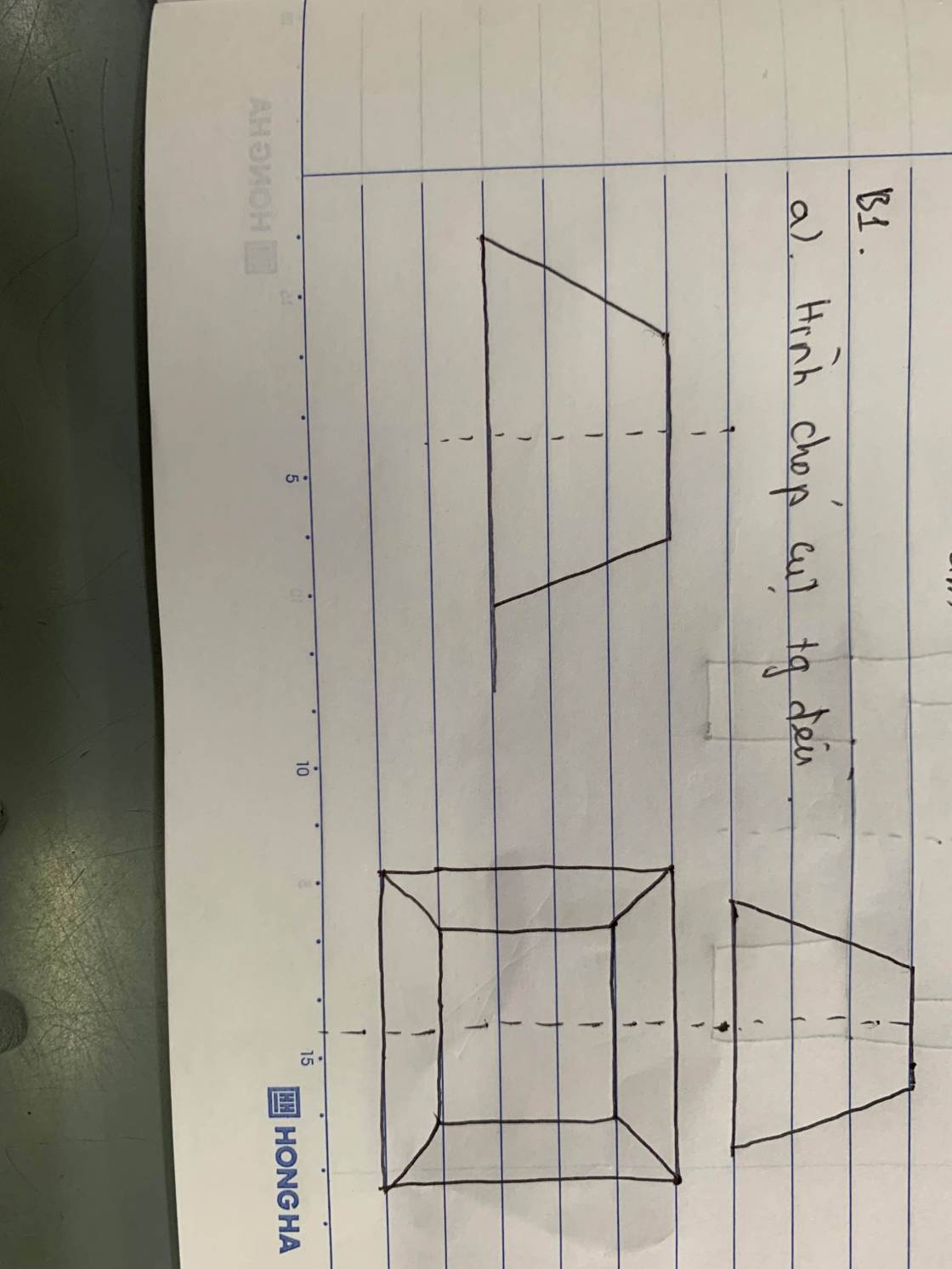


 giúp t với ạ
giúp t với ạ ì làm giùm mình câu này với ạ
ì làm giùm mình câu này với ạ 

 giúp mình với ạ
giúp mình với ạ
Gọi O là giao điểm AC và BD \(\Rightarrow H\in BO\Rightarrow H\in BD\) do tam giác ABC đều
\(\Rightarrow SH\in\left(SBD\right)\)
Ta có: \(\left\{{}\begin{matrix}AC\perp BD\left(\text{2 đường chéo hình thoi}\right)\\SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\end{matrix}\right.\)
\(\Rightarrow AC\perp\left(SBD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow SH\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBH}\) là góc giữa SB và (ABCD)
\(BH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow tan\widehat{SBH}=\dfrac{SH}{BH}=\sqrt{6}\) \(\Rightarrow\widehat{SBH}\approx67^048'\)
Theo cm câu a ta có \(AC\perp\left(SBD\right)\) tại O
\(\Rightarrow SO\) là hình chiếu vuông góc của SC lên (SBD)
\(\Rightarrow\widehat{CSO}\) là góc giữa SC và (SBD)
\(OC=\dfrac{1}{2}AC=\dfrac{a}{2}\)
\(OH=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\Rightarrow SO=\sqrt{SH^2+OH^2}=\dfrac{5a\sqrt{3}}{6}\)
\(\Rightarrow tan\widehat{CSO}=\dfrac{OC}{SO}=\dfrac{\sqrt{3}}{5}\Rightarrow\widehat{CSO}\approx19^0\)