
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$

\(\left|x+1\right|và\left|x+2\right|\ge0\)
\(\Rightarrow\orbr{\begin{cases}\left(x+1\right)+\left(x+2\right)=3\\\left(x+1\right)+\left(x+2\right)=-3\end{cases}}\)
\(\orbr{\begin{cases}2x+3=3\\2x+3=-3\end{cases}}\)
\(\orbr{\begin{cases}2x=0\\2x=-6\end{cases}}\)
\(\orbr{\begin{cases}x=0\\x=-3\end{cases}}\)
\(\left|x+1\right|+\left|x+2\right|=3\)
Xét \(x+1\ge0;x+2\ge0\Leftrightarrow x\ge-1;x\ge-2\Rightarrow x\ge-1\) ta có : \(\hept{\begin{cases}\left|x+1\right|=x+1\\\left|x+2\right|=x+2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=3\Leftrightarrow x+1+x+2=3\Leftrightarrow2x+3=3\Rightarrow x=0\)(TM)
Xét \(x+1\le0;x+2\ge0\Leftrightarrow-2\le x\le-1\) ta có : \(\hept{\begin{cases}\left|x+1\right|=-x-1\\\left|x+2\right|=x+2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=3\Leftrightarrow-x-1+x+2=3\Leftrightarrow1=3\) (loại)
Xét \(x+1\le0;x+2\le0\Leftrightarrow x\le-1;x\le-2\Leftrightarrow x\le-2\) ta có : \(\hept{\begin{cases}\left|x+1\right|=-x-1\\\left|x+2\right|=-x-2\end{cases}}\)
\(\Rightarrow\left|x+1\right|+\left|x+2\right|=-x-1-x-2=-2x-3=3\Rightarrow x=-3\)(TM)
Vậy \(x=\left\{-3;0\right\}\)

Để M là số nguyên
Thì (x2–5) chia hết cho (x2–2)
==>(x2–2–3) chia hết cho (x2–2)
==>[(x2–2)—3] chia hết cho (x2–2)
Vì (x2–2) chia hết cho (x2–2)
Nên 3 chia hết cho (x2–2)
==> (x2–2)€ Ư(3)
==> (x2–2) €{1;-1;3;-3}
TH1: x2–2=1
x2=1+2
x2=3
==> ko tìm được giá trị của x
TH2: x2–2=-1
x2=-1+2
x2=1
12=1
==>x=1
TH3: x2–2=3
x2=3+2
x2=5
==> không tìm được giá trị của x
TH4: x2–2=-3
x2=-3+2
x2=-1
(-1)2=1
==> x=-1
Vậy x € {1;—1)

Ta có : \(\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{5}}\)
\(\Rightarrow\frac{x\times y}{\frac{1}{3}\times\frac{1}{5}}=\frac{1500}{\frac{1}{15}}=22500\)
\(\Rightarrow\frac{x}{\frac{1}{3}}=22500\Rightarrow x=22500\times\frac{1}{3}=7500\)
\(\Rightarrow\frac{y}{\frac{1}{5}}=22500\Rightarrow y=22500\times\frac{1}{5}=4500\)

\(\dfrac{x}{y}=\dfrac{6}{5}\)⇒\(\dfrac{x}{6}=\dfrac{y}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{x+y}{6+5}=\dfrac{121}{11}=11\)
⇒\(x=66;y=55\)

\(Q\left(x\right)-P\left(x\right)=0\)
\(\Leftrightarrow\left(-6x^2+x^3-8+12\right)-\left(x^3-3x^2+6x-8\right)=0\)
\(\Leftrightarrow\left(-6x^2+x^3+4\right)-\left(x^3-3x^2+6x-8\right)=0\)
\(\Leftrightarrow-6x^2+x^3+4-x^3+3x^2-6x+8=0\)
\(\Leftrightarrow-3x^2-6x+12=0\)
\(\Leftrightarrow-3\left(x^2+2x-4\right)=0\)
\(\Leftrightarrow x^2+2x-4=0\)
\(\Leftrightarrow x^2+2x+1=5\)
\(\Leftrightarrow\left(x+1\right)^2=5\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=\sqrt{5}\\x+1=-\sqrt{5}\end{cases}}\Leftrightarrow x=\pm\sqrt{5}-1\)
\(P\left(x\right)-Q\left(x\right)=\left(x^3-3x^2+6x-8\right)-\left(-6x^2+x^3-8+12\right)\)
\(P\left(x\right)-Q\left(x\right)=\left(x^3-3x^2+6x-8\right)-\left(-6x^2+x^3+4\right)\)
\(P\left(x\right)-Q\left(x\right)=x^3-3x^2+6x-8+6x^2-x^3-4\)
\(P\left(x\right)-Q\left(x\right)=3x^2+6x-4\)
Ta cần phân tích \(3x^2+6x-4\) thành nhân tử
Ta có:\(P\left(x\right)-Q\left(x\right)=-\frac{1}{3}\left(-9x^2-18x+12\right)\)
\(=-\frac{1}{3}\left[21-\left(9x^2+18x+9\right)\right]\)
\(=-\frac{1}{3}\left[21-\left(3x+3\right)^2\right]\)
\(=-\frac{1}{3}\left(\sqrt{21}-3x-3\right)\left(\sqrt{21}+3x+3\right)\)
\(\Rightarrow x=\frac{\sqrt{21}-3}{3};x=\frac{-\sqrt{21}-3}{3}\)

a, Vì \(\left\{{}\begin{matrix}AN=NC\\\widehat{AND}=\widehat{BNC}\left(đối.đỉnh\right)\\BN=ND\end{matrix}\right.\) nên \(\Delta AND=\Delta CNB\left(c.g.c\right)\)
Do đó \(AD=BC\)
b, Vì \(\left\{{}\begin{matrix}AM=MB\\\widehat{AME}=\widehat{BMC}\left(đối.đỉnh\right)\\EM=MC\end{matrix}\right.\) nên \(\Delta AME=\Delta BMC\left(c.g.c\right)\)
Do đó \(\widehat{MAE}=\widehat{MBC}\) mà 2 góc này ở vị trí so le trong nên AE//BC
c, Vì \(\widehat{NAD}=\widehat{NCB}\left(\Delta AND=\Delta CNB\right)\) mà 2 góc này ở vị trí slt nên AD//BC
Mà AE//BC nên A,D,E thẳng hàng
Ta có \(AE=BC\left(\Delta AME=\Delta BMC\right)\)
Mà \(AD=BC\left(cmt\right)\) nên \(AD=AE\)
Vậy A là trung điểm DE


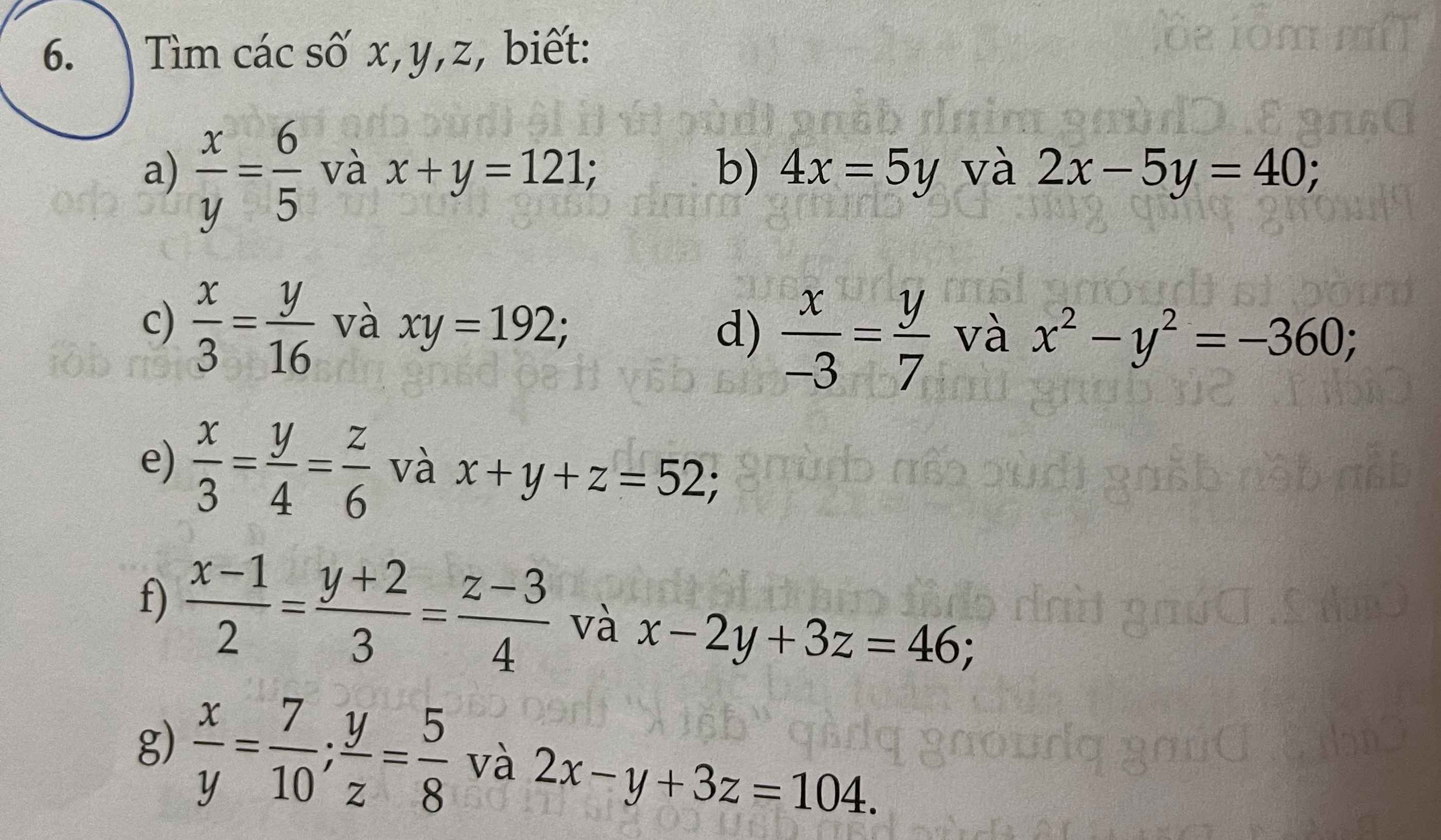
Giải:
Gọi số học sinh của mỗi nhóm lần lượt là: \(x;y;z\) (học sinh); \(x;y;z\)\(\in\)N*
Theo bài ra ta có:
4\(x\) = 6y = 12z và \(x+y+z\) = 42
4\(x\) = 6y ⇒ \(x\) = \(\dfrac{6}{4}\)y= \(\dfrac{3}{2}y\); 6y = 12z ⇒ z = \(\dfrac{6y}{12}\) = \(\dfrac{1}{2}\) y
Thay \(x=\)\(\dfrac{3}{2}y\); z = \(\dfrac{1}{2}y\) vào biểu thức: \(x+y+z\) = 42 ta có:
\(\dfrac{3}{2}y+y+\dfrac{1}{2}y=42\)
y.(\(\dfrac{3}{2}+1+\dfrac{1}{2}\)) = 42
y.3 = 42
y = 42 : 3
y = 14 (1)
thay y = 1 vào biểu thức: \(x\) = \(\dfrac{3}{2}y\) ⇒ \(x\) = 14.\(\dfrac{3}{2}=21\) (2)
Thay y = 14 vào biểu thức z = \(\dfrac{1}{2}y=\) 14.\(\dfrac{1}{2}\) = 7 (3)
Từ (1); (2); (3) ta có: \(\left(x;y;z\right)\) = (21; 14; 7)
Kết luận số học sinh tổ 1;tổ 2; tổ 3 lần lượt là: 21học sinh; 14 học sinh; 7 học sinh.
Gọi a (học sinh), b (học sinh), c (học sinh) lần lượt là số học sinh của nhóm I, nhóm II, nhóm III (a, b, c ∈ ℕ*)
Do năng suất trồng cây của mỗi học sinh là như nhau và cùng trồng một số cây như nhau nên số học sinh và số ngày hoàn thành là hai đại lượng tỉ lệ nghịch
⇒ 4a = 6b = 12c
⇒ a/3 = b/2 = c/1
Do tổng số học sinh là 42 nên a + b + c = 42
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/3 = b/2 = c/1 = (a + b + c)/(3 + 2 + 1) = 42/6 = 7
a/3 = 7 ⇒ a = 7.3 = 21 (nhận)
b/2 = 7 ⇒ b = 7.2 = 14 (nhận)
c/1 = 7 ⇒ c = 7.1 = 7 (nhận)
Vậy số học sinh của nhóm I, nhóm II, nhóm III lần lượt là: 21 học sinh, 14 học sinh, 7 học sinh