
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


) 120 độ z' x' O z y x
thực ra bữa h off bây h rảnh nên vào lướt hoidap -.- thấy bài bạn nên làm vậy
a) Vì Oz là tia phân giác của xOy
=> xOz = zOy =\(\frac{xOy}{2}=\frac{120^0}{2}=60^0\)
Vì x'Oz' đối đính xOz
=> x'Oz' = xOz= 60 độ
làm tới đây thôi nhé mình phải đi ngủ rồi , còn mỗi câu b mấy bạn khác làm luôn đi.

Cho mình làm lại
TL:
Có 2 số nguyên thoả mãn là :
X + Y = 7
HT

Bài 4
a/ \(x=\widehat{ABC};y=\widehat{ADC}\)
Ta có a//b; \(a\perp c\Rightarrow b\perp c\Rightarrow x=\widehat{ABC}=90^o\)
Xét tứ giác ABCD
\(y=\widehat{ADC}=360^o-\widehat{BAD}-\widehat{ABC}-\widehat{BCD}\) (tổng các góc trong của tứ giác = 360 độ)
\(\Rightarrow y=\widehat{ADC}=360^o-90^o-90^o-130^o=50^o\)
b/ Kéo dài n về phí B cắt AC tại D
\(\Rightarrow\widehat{CBD}=180^o-\widehat{nBC}=180^o-105^o=75^o\)
Xét tg BCD có
\(\widehat{BDC}=180^o-\widehat{CBD}-\widehat{BCD}=180^o-75^o-60^o=45^o=\widehat{mAC}\)
=> Am//Bn (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành hai góc đồng vị bằng nhau thì chúng // với nhau)
Bài 5
\(\frac{a}{3b}=\frac{b}{3c}=\frac{c}{3a}=\frac{a+b+c}{3\left(a+b+c\right)}=\frac{1}{3}\)
Ta có \(\frac{a}{3b}=\frac{b}{3c}=\frac{a+b}{3\left(b+c\right)}=\frac{1}{3}\Rightarrow\frac{a+b}{b+c}=1\Rightarrow a+b=b+c\)
\(\frac{b}{3c}=\frac{c}{3a}=\frac{b+c}{3\left(c+a\right)}=\frac{1}{3}\Rightarrow\frac{b+c}{c+a}=1\Rightarrow b+c=c+a\)
\(\Rightarrow a+b=b+c=c+a\)
\(\frac{c}{3a}=\frac{a}{3b}=\frac{c+a}{3\left(a+b\right)}=\frac{1}{3}\Rightarrow\frac{c+a}{a+b}=1\)
Từ \(\frac{a+b}{b+c}=\frac{a}{b+c}+\frac{b}{b+c}=\frac{a}{b+c}+\frac{b}{c+a}=1\) (1)
Từ \(\frac{b+c}{c+a}=\frac{b}{c+a}+\frac{c}{c+a}=\frac{b}{c+a}+\frac{c}{a+b}=1\) (2)
Từ \(\frac{c+a}{a+b}=\frac{c}{a+b}+\frac{a}{a+b}=\frac{c}{a+b}+\frac{a}{b+c}=1\) (3)
Công 2 vế của (1) (2) và (3)
\(\Rightarrow\frac{a}{b+c}+\frac{b}{c+a}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{c}{a+b}+\frac{a}{b+c}=3\)
\(\Rightarrow2\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)=3.\)
\(\Rightarrow\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}=\frac{3}{2}\)
\(\Rightarrow M=2018\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)=\frac{2018.3}{2}=3027\)

ta có : Do NB song song với MA nên
\(\hept{\begin{cases}\widehat{ABN}+\widehat{MAB}=180^0\\\widehat{ABN}-\widehat{MAB}=40^0\end{cases}}\Rightarrow2\widehat{MAB}=180^0-40^0=140^0\)
Nên \(\widehat{MAB}=70^0\)

Bài 3 :
A B S M C P N x y 1 2 z 1 2
a) Kéo dài tia NM và NM cắt BC tại S
Khi đó ta có :
\(\hept{\begin{cases}\widehat{ABC}=\widehat{BSM}\left(\text{ 2 góc so le trong }\right)\\\widehat{MNP}=\widehat{BSM}\left(\text{ 2 góc so le trong }\right)\end{cases}}\Rightarrow\widehat{ABC}=\widehat{MNP}\Rightarrow\widehat{MNP}=40^o\)
b) Vẽ \(\hept{\begin{cases}\text{Bx là tia phân giác của }\widehat{ABC}\\\text{Ny là tia phân giác của }\widehat{MNP}\end{cases}}\)
\(\Rightarrow\widehat{B_1}=B_2=\widehat{N_1}=\widehat{N_2}=\frac{\widehat{ABC}}{2}=\frac{\widehat{MNP}}{2}=\frac{40^o}{2}=20^o\left(\text{do }\widehat{ABC}=\widehat{MNP}\right)\)
Vẽ Sz // Bx => \(\widehat{B_2}=\widehat{S_1}\)
Lại có \(\widehat{BSN}=\widehat{MSP}\Rightarrow\frac{\widehat{BSN}}{2}=\frac{\widehat{MSP}}{2}\Rightarrow\widehat{S_2}=\widehat{N_1}\)mà \(\widehat{S_2}\text{ và }\widehat{N_1}\)là 2 góc so le trong
=> Sz // Ny mà Sz // Bx => Bx // Ny hay tia phân giác của 2 góc \(\widehat{ABC}\text{ và }\widehat{MNP}\)song song nhau

3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau

Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)

Câu 1
a) Vì m vuông góc vớiAB }=> m// n
N vuông góc với AB
Vậy...
b) vì m//n(a)
=> ADC +C1=180°( 2 góc trong cùng phía)
=>120°+C1=180°
=> C1
=60°
Vậy...
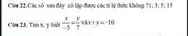













 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ

 ới ạ đang gấp lắm
ới ạ đang gấp lắm
Câu 22:
Có.Vì \(1.15=3.5\left(=15\right)\) nên ta có thể lập tỉ lệ thức từ các số đã cho
VD:\(\dfrac{1}{3}=\dfrac{5}{15}\)
Câu 23:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=-5.7=-35\end{matrix}\right.\)
Vậy....
oki cảm ơn !