
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(x^2-7=\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\)
b: \(x^2-2x\sqrt{2}+2=\left(x-\sqrt{2}\right)^2\)
c: \(x^2+2x\sqrt{13}+13=\left(x+\sqrt{13}\right)^2\)

\(\Rightarrow\left\{{}\begin{matrix}x+my=m+1\\m^2x+my=2m^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+my=m+1\\\left(m^2-1\right)x=2m^2-m-1\end{matrix}\right.\)
Phương trình có nghiệm duy nhất khi \(m^2-1\ne0\Rightarrow m\ne\pm1\)
Khi đó ta có: \(x=\dfrac{2m^2-m-1}{m^2-1}=\dfrac{\left(m-1\right)\left(2m+1\right)}{\left(m-1\right)\left(m+1\right)}=\dfrac{2m+1}{m+1}\)
\(\Rightarrow y=2m-mx=\dfrac{m}{m+1}\)
Để \(\left\{{}\begin{matrix}x\ge2\\y\ge1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{2m+1}{m+1}\ge2\\\dfrac{m}{m+1}\ge1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{-1}{m+1}\ge0\\\dfrac{-1}{m+1}\ge0\end{matrix}\right.\)
\(\Rightarrow m+1< 0\Rightarrow m< -1\)


\(1,x=9\Rightarrow A=\dfrac{2\sqrt{9}+1}{\sqrt{9}}=\dfrac{2.3+1}{3}=\dfrac{7}{3}\)
\(2,B=\dfrac{x-3\sqrt{x}+4}{x-2\sqrt{x}}-\dfrac{1}{\sqrt{x}-2}\left(dk:x>0,x\ne4\right)\\ =\dfrac{x-3\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}-\dfrac{1}{\sqrt{x}-2}\\ =\dfrac{x-3\sqrt{x}+4-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{x-4\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(3,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-2}{\sqrt{x}}:\dfrac{2\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\)
Ta có : \(\left|P\right|+P=0\Leftrightarrow\left|P\right|=-P\)
\(TH_1:x\ge4\\ \dfrac{\sqrt{x}-2}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\Leftrightarrow\dfrac{2\left(\sqrt{x}-2\right)}{2\sqrt{x}+1}=0\Leftrightarrow2\sqrt{x}=4\Leftrightarrow x=4\left(tm\right)\)
\(TH_2:x< 4\\ -\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\left(LD\right)\)
Vậy \(x=4\) thì thỏa mãn đề bài.

\(B=\sqrt{14+2\sqrt{10}+2\sqrt{14}+2\sqrt{35}}\)
\(=\sqrt{2}+\sqrt{5}+\sqrt{7}\)

\(P=\dfrac{x-\sqrt{x}+\sqrt{x}-3-\sqrt{x}-3}{x-9}\)
\(=\dfrac{x-\sqrt{x}-6}{x-9}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{x-9}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\)
4:
a: P>4/5
=>P-4/5>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{4}{5}>0\)
=>\(\dfrac{5\sqrt{x}+10-4\sqrt{x}-12}{5\sqrt{x}+15}>0\)
=>\(\sqrt{x}-2>0\)
=>x>4
b: \(P>\dfrac{2\sqrt{x}}{5}\)
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{2\sqrt{x}}{5}>0\)
=>\(\dfrac{5\sqrt{x}+10-2x-6\sqrt{x}}{5\sqrt{x}+15}>0\)
=>\(-2x-\sqrt{x}+10>0\)
=>\(-2x-5\sqrt{x}+4\sqrt{x}+10>0\)
=>\(\left(2\sqrt{x}+5\right)\left(-\sqrt{x}+2\right)>0\)
=>\(-\sqrt{x}+2>0\)
=>0<=x<4
5:
a: \(P-\dfrac{1}{2}=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{1}{2}\)
\(=\dfrac{2\sqrt{x}+4-\sqrt{x}-3}{2\sqrt{x}+6}=\dfrac{\sqrt{x}+1}{2\sqrt{x}+6}>0\)
=>P>1/2
b: \(P-1=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-1=\dfrac{\sqrt{x}+2-\sqrt{x}-3}{\sqrt{x}+3}\)
\(=\dfrac{-1}{\sqrt{x}+3}< 0\)
\(P^2-P=P\left(P-1\right)\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\cdot\dfrac{-1}{\sqrt{x}+3}< 0\)
=>P^2<P
=>P>P^2

làm như giỏi lắm í, thôi khỏi nói cũng biết, ko cần thể hiện đâu
\(A=\frac{a}{\sqrt{3+a^2}}+\frac{b}{\sqrt{3+b^2}}+\frac{c}{\sqrt{3+c^2}}\)
\(=\frac{a+b+c}{\sqrt{3+a^2}+\sqrt{3+b^2}+\sqrt{3+c^2}}\)
Ta có: \(\sqrt{3+a^2}+\sqrt{3+b^2}+\sqrt{3+c^2}\)
\(=\sqrt{ab+bc+ac+a^2}+\sqrt{ab+bc+ac+b^2}+\sqrt{ab+bc+ca+c^2}\)
\(=\sqrt{b\left(a+c\right)+a\left(a+c\right)}+\sqrt{b\left(a+b\right)+c\left(a+b\right)}+\sqrt{b\left(a+c\right)+c\left(a+c\right)}\)
\(=\sqrt{\left(a+c\right)\left(a+b\right)}+\sqrt{\left(a+b\right)\left(b+c\right)}+\sqrt{\left(a+c\right)\left(b+c\right)}\)
\(\le\frac{a+c+a+b}{2}+\frac{a+b+b+c}{2}+\frac{a+c+b+c}{2}\)
\(\le\frac{2a+a+2b+b+2c+c}{2}=\frac{3a+3b+3c}{2}=\frac{3}{2}\left(a+b+c\right)\)
Suy ra : \(A=\frac{a+b+c}{\sqrt{3+a^2}+\sqrt{3+b^2}+\sqrt{3+c^2}}\ge\frac{2}{3}\)
Dấu "=" xảy ra khi và chỉ khi a=b=c=0
Vậy Amin = \(\frac{2}{3}\)
Chắc sai. Mong bạn giúp đỡ. Cảm ơn!

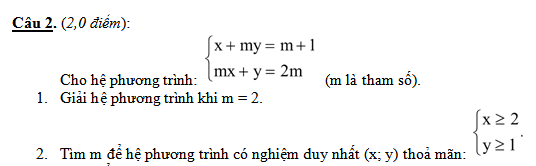

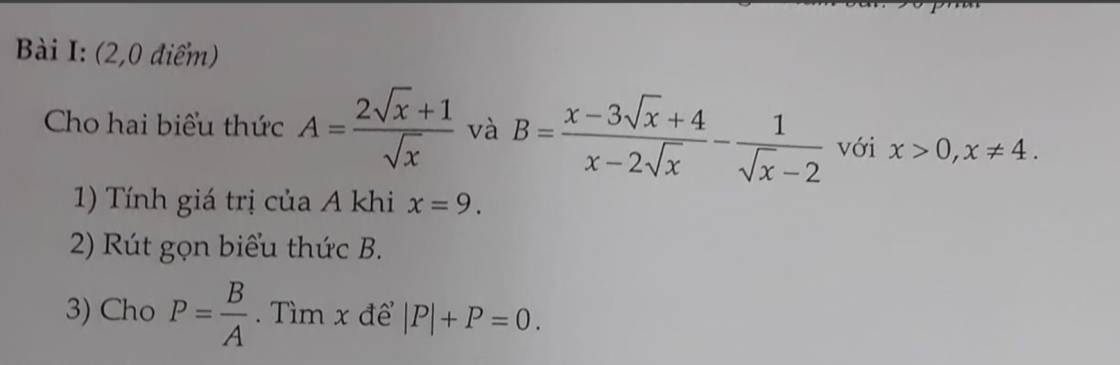



Cậu bổ sung đề nha