
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
BD=CE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AB=AC
hay ΔABC cân tại A
b: XétΔABC có
AD là đường cao
CH là đường cao
AD cắt CH tại D
Do đó: D là trực tâm của ΔABC
=>BD vuông góc với AC

Ban chi mk cach tim gia tri nho nhat / lon nhat cho mk nha


\(\frac{B}{A}=\frac{2^2+4^2+6^2+...+200^2}{1^2+2^2+...+100^2}=\frac{\left(1.2\right)^2+\left(2.2\right)^2+...+\left(100.2\right)^2}{1^2+2^2+...+100^2}\)
\(=\frac{1^2.2^2+2^2.2^2+...+100^2+2^2}{1^2+2^2+...+100^2}\)
\(=\frac{\left(1^2+2^2+...+100^2\right).2^2}{1^2+2^2+100^2}\)
\(=2^2=4\)
Vậy \(\frac{B}{A}=4\)
Sửa lại: ( tại nhìn bé quá, tưởng mũ 3 -> mũ 2 )
\(\frac{B}{A}=\frac{2^3+4^3+6^3+...+200^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{\left(1.2\right)^3+\left(2.2\right)^3+...+\left(100.2\right)^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{1^3.2^3+2^3.2^3+...+100^3.2^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{\left(1^3+2^3+...+100^3\right)2^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=2^3=8\)
Vậy \(\frac{B}{A}=8\)

\(\left\{{}\begin{matrix}\widehat{CBA}< 135\Rightarrow\widehat{ABD}>45\Rightarrow\widehat{BAD}< 45\Rightarrow BD< DA\\\widehat{ACD}< 45\Rightarrow\widehat{CAD}>45\Rightarrow AD< CD\\\end{matrix}\right.\)
Làm toán hình thì phải lập luận rõ ràng, trong toán hình cái điểm lập luận là cao nhất, nếu không có thì 0 điểm, chế làm như vậy có phải đẩy người ta xuống 0 điểm không? Làm ơn bỏ ngay cái ngoặc tròn (và) của lớp 8 đi!

\(x-y=9\Rightarrow x=9+y\Rightarrow y=x-9\)
Ta có:
\(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)
\(=\dfrac{3x+x-9}{3x+y}-\dfrac{3y+y+9}{3y+x}\)
\(=\dfrac{3x+\left(x-9\right)}{3x+y}-\dfrac{3y+\left(y+9\right)}{3y+x}\)
\(=\dfrac{3x+y}{3x+y}-\dfrac{3y+x}{3y+x}\)
\(=1-1\)
\(=0\)
Vậy biểu thức \(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)khi \(x-y=9\) là 0
\(x-y=9\Rightarrow y=x-9\) thay vào biểu thức B ta được :
\(B=\dfrac{4x-9}{3x+\left(x-9\right)}-\dfrac{4\left(x-9\right)+9}{3\left(x-9\right)+x}=\dfrac{4x-9}{4x-9}-\dfrac{4x-27}{4x-27}=1-1=0\)
Vậy giá trị của B là 0 tại \(x-y=9\)

Ta có tam giác MNP có 3 đg phân giác cùng cắt nhau tại I
->PI là đg phân giác của góc MPN ( đ.lý về 3 đg phân giác của 1 tam giác)
Mặt khác gócMPN bằng 70 độ-> gócIPH= MNP/2=70/2=35 độ
Vậy....
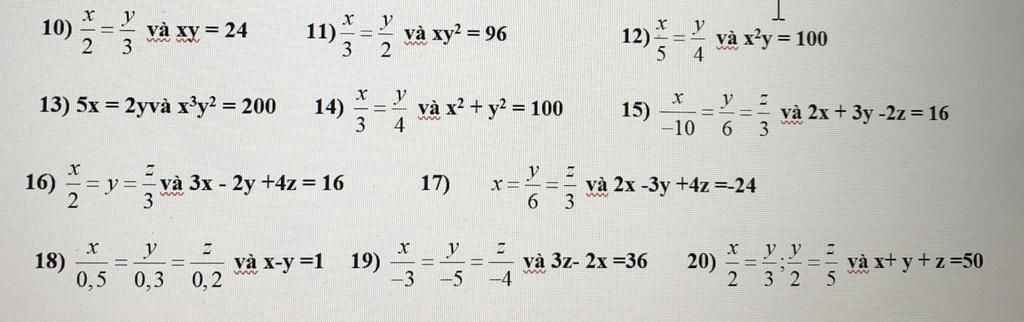































14) \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x^2}{3^2}=\dfrac{y^2}{4^2}\)
Theo tính chất của DTSBN, ta được :
\(\dfrac{x^2}{3^2}=\dfrac{y^2}{4^2}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=4.3^2=36\\y^2=4.4^2=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\pm6\\y=\pm8\end{matrix}\right.\)
Vì x,y cùng dấu nên cặp số (x ; y) = (6 ; 8) ; (-6 ; - 8)
12, Ta có : \(\dfrac{x}{5}=\dfrac{y}{4}\)
\(\Rightarrow y=\dfrac{4}{5}x\)
- Thay y vào biểu thức trên ta được ; \(\dfrac{4}{5}x^3=100\)
\(\Rightarrow x=5\)
\(\Rightarrow y=4\)
Vậy...
14, Ta có : \(\dfrac{x}{3}=\dfrac{y}{4}\)
\(\Rightarrow\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{25}=4\) ( Tính chất dãy tỉ số bằng nhau )
\(\Rightarrow\left\{{}\begin{matrix}x=\pm6\\y=\pm8\end{matrix}\right.\)
Vậy ...