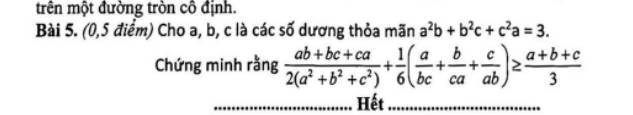K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 8 2021
Kẻ \(BH\perp DC\) tại H
Dễ cm được \(ABHD\) là hình vuông(do ABHD là có ba góc vuông và hai cạnh kề bằng nhau)
\(\Rightarrow BH=HD=8\)m
Có \(tanC=\dfrac{BH}{HC}\Leftrightarrow tan45^0=\dfrac{8}{HC}\Leftrightarrow HC=8\left(m\right)\)
Có \(sinC=\dfrac{BH}{BC}\Leftrightarrow sin45^0=\dfrac{8}{BC}\Leftrightarrow BC=8\sqrt{2}\left(m\right)\)
Chu vi hình thang là:
\(C=AB+BC+CD+AD=8+8\sqrt{2}+CH+HD+AD=8+8\sqrt{2}+8+8+8=32+8\sqrt{2}\left(m\right)\)
Ý A
NQ
0
HB
2
12 tháng 10 2021
\(\left(3\sqrt{7}\right)^2=63>28=\left(\sqrt{28}\right)^2\) hoặc \(3\sqrt{7}>2\sqrt{7}=\sqrt{28}\)
HH
3
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
\(\sqrt{21}-4\sqrt{5}\) thì đâu có rút gọn được giống giá trị nào trong số các đáp án đâu em?
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
Ta có:
\(\dfrac{ab+bc+ca}{2\left(a^2+b^2+c^2\right)}+\dfrac{1}{6}\left(\dfrac{a^2+b^2+c^2}{abc}\right)\ge2\sqrt{\dfrac{1}{12}\left(\dfrac{ab+ca+ca}{abc}\right)}=\sqrt{3\left(\dfrac{ab+bc+ca}{abc}\right)}\)
Nên ta chỉ cần cm:
\(\sqrt{\dfrac{1}{3}\left(\dfrac{ab+bc+ca}{abc}\right)}\ge\dfrac{a+b+c}{3}\Leftrightarrow3\left(\dfrac{ab+bc+ca}{abc}\right)\ge\left(a+b+c\right)^2\)
Thật vậy, ta có:
\(\dfrac{3\left(ab+bc+ca\right)}{abc}=\dfrac{\left(a^2b+b^2c+c^2a\right)\left(ab+bc+ca\right)}{abc}\)
\(=\left(\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{c}{b}\right)\left(ac+ab+bc\right)\ge\left(a+b+c\right)^2\) (Bunhiacopxki)
Dấu "=" xảy ra khi \(a=b=c=1\)