
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(1,\\ a,x=\dfrac{\sqrt{3}-\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}=0\\ \Leftrightarrow A=\left(0-0-1\right)^2+2021=1+2021=2022\\ b,\left(x+\sqrt{x^2+2021}\right)\left(y+\sqrt{y^2+2021}\right)=2021\\ \Leftrightarrow\left(x-\sqrt{x^2+2021}\right)\left(x+\sqrt{x^2+2021}\right)\left(y+\sqrt{y^2+2021}\right)=2021\left(x-\sqrt{x^2+2021}\right)\\ \Leftrightarrow-2021\left(y+\sqrt{y^2+2021}\right)=2021\left(x-\sqrt{x^2+2021}\right)\)
Cmttt \(\Leftrightarrow-2021\left(x+\sqrt{x^2+2021}\right)=2021\left(y-\sqrt{y^2+2021}\right)\)
Cộng vế theo vế
\(\Leftrightarrow-2021y-2021\sqrt{y^2+2021}-2021x-2021\sqrt{x^2+2021}=2021x-2021\sqrt{x^2+2021}+2021y-2021\sqrt{y^2+2021}\\ \Leftrightarrow x+y=0\\ \Leftrightarrow x=-y\\ \Leftrightarrow x^{2021}+y^{2021}=x^{2021}-x^{2021}=0\)

3:
1: Đặt căn x-3=a; |2y-1|=b
Theo đề, ta có: 8/a+1/b=5 và 4/a+1/b=3
=>a=2 và b=1
=>căn x=5 và |2y-1|=1
=>x=25 và \(y\in\left\{1;0\right\}\)
2:
mx-2y=2m và -2x+y=m+1
=>mx-2y=2m và -4x+2y=2m+2
=>(m-4)x=4m+2 và y=-2x-m-1
=>x=(4m+2)/(m-4) và \(y=\dfrac{-8m-4}{m-4}-m-1\)
x=y
=>\(\dfrac{4m+2}{m-4}=\dfrac{-8m-4}{m-4}-m-1\)
=>\(\dfrac{4m+2+8m+4}{m-4}=-m-1\)
=>(m-4)(-m-1)=12m+6
=>-m^2-m+4m+4-12m-6=0
=>-m^2-9m-2=0
=>\(m=\dfrac{-9\pm\sqrt{73}}{2}\)


\(1,\\ a,=5\sqrt{2}-12\sqrt{2}+10\sqrt{2}=3\sqrt{2}\\ b,=\dfrac{\sqrt{5}-2}{5-4}-\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{\sqrt{3}-2}=\sqrt{5}-2-\sqrt{5}=-2\\ c,=3\sqrt{3}-\left|1-\sqrt{3}\right|-\dfrac{6\sqrt{3}}{3}=3\sqrt{3}-\left(\sqrt{3}-1\right)-2\sqrt{3}=1\)
\(2,\\ a,P=\left(\dfrac{1}{\sqrt{a}-2}+\dfrac{1}{\sqrt{a}+2}\right)\left(1+\dfrac{2\left(\sqrt{a}-2\right)}{a-2\sqrt{a}}\right)\left(a>0;a\ne4\right)\\ P=\dfrac{\sqrt{a}+2+\sqrt{a}-2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\cdot\left[1+\dfrac{2\left(\sqrt{a}-2\right)}{\sqrt{a}\left(\sqrt{a}-2\right)}\right]\\ P=\dfrac{2\sqrt{a}}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\cdot\dfrac{\sqrt{a}+2}{\sqrt{a}}=\dfrac{2}{\sqrt{a}-2}\)
\(b,\sqrt{4x+12}-3\sqrt{x+3}+\sqrt{16x+48}=9\left(x\ge-3\right)\\ \Leftrightarrow2\sqrt{x+3}-3\sqrt{x+3}+4\sqrt{x+3}=9\\ \Leftrightarrow3\sqrt{x+3}=9\Leftrightarrow\sqrt{x+3}=3\\ \Leftrightarrow x+3=9\Leftrightarrow x=6\left(tm\right)\)


Bài 3:
a: Thay x=9 vào A, ta được:
\(A=\dfrac{3-2}{3+3}=\dfrac{1}{6}\)

Bài 3:
\(1,x=9\Leftrightarrow A=\dfrac{3-2}{9+3}=\dfrac{1}{12}\\ 2,P=AB=\dfrac{\sqrt{x}-2}{x+3}\cdot\dfrac{x-3\sqrt{x}+2-2+5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(x+3\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{x+3}\\ 3,\left(10x+30\right)P\ge x+25\\ \Leftrightarrow\dfrac{3\sqrt{x}\left(x+3\right)}{x+3}-x-25\ge0\\ \Leftrightarrow3\sqrt{x}-x-25\ge0\\ \Leftrightarrow-\left(x-3\sqrt{x}+\dfrac{9}{4}\right)-\dfrac{91}{4}\ge0\\ \Leftrightarrow-\left(\sqrt{x}-\dfrac{3}{2}\right)^2-\dfrac{91}{4}\ge0\left(vô.lí\right)\\ \Leftrightarrow x\in\varnothing\)

Bài 1 :
\(...\Rightarrow A=\dfrac{\sqrt[]{x}\left(\sqrt[]{x}+2\right)+\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}-2\right)}{\left(\sqrt[]{x}-2\right)\left(\sqrt[]{x}+2\right)}-\dfrac{\sqrt[]{x}-10}{x-4}\)
\(\Rightarrow A=\dfrac{x+2\sqrt[]{x}+x-3\sqrt[]{x}+2}{x-4}-\dfrac{\sqrt[]{x}-10}{x-4}\)
\(\Rightarrow A=\dfrac{2x-\sqrt[]{x}+2-\sqrt[]{x}+10}{x-4}\)
\(\Rightarrow A=\dfrac{2x-2\sqrt[]{x}+12}{x-4}=\dfrac{2\left(x-\sqrt[]{x}+6\right)}{x-4}\)






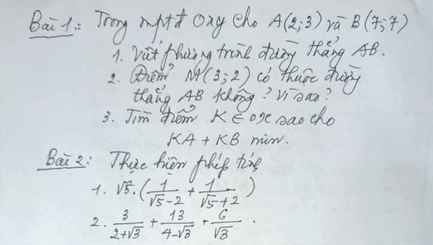 làm hộ mik bài 1 thôi nha
làm hộ mik bài 1 thôi nha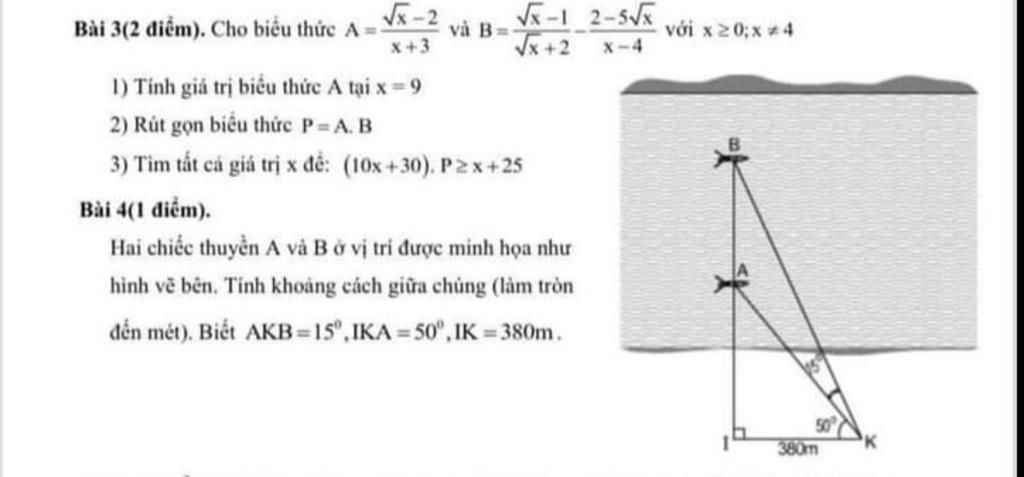
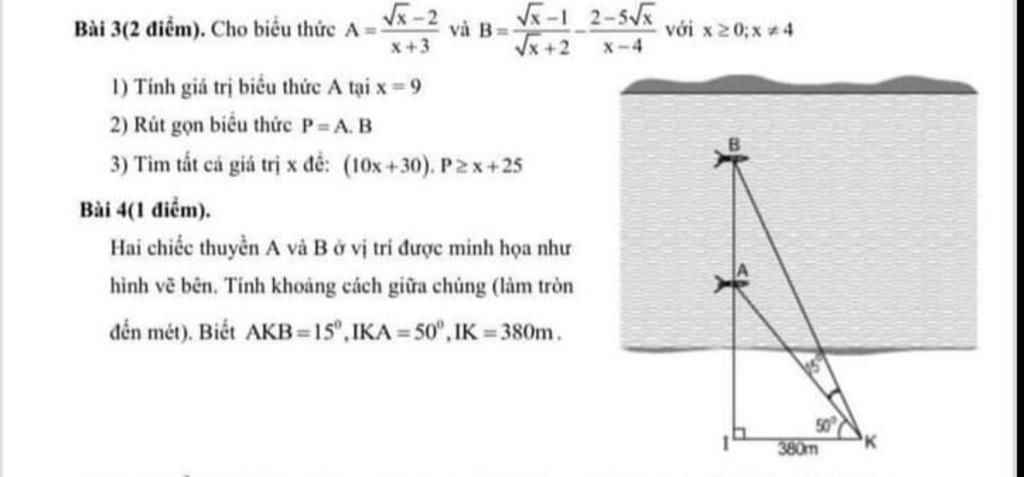

18b:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x+5>=0\\x>=0\end{matrix}\right.\Leftrightarrow x>=0\)
\(\sqrt{x+5}=1+\sqrt{x}\)
=>\(\left(\sqrt{x+5}\right)^2=\left(1+\sqrt{x}\right)^2\)
=>\(x+2\sqrt{x}+1=x+5\)
=>\(2\sqrt{x}=4\)
=>\(\sqrt{x}=2\)
=>x=4(nhận)
b: ĐKXĐ: 2x+1>=0
=>\(x>=-\dfrac{1}{2}\)
\(5\sqrt{2x+1}+\dfrac{7}{3}\sqrt{18x+9}-\sqrt{8x+4}-\sqrt{2x+1}=18\)
=>\(4\sqrt{2x+1}+\dfrac{7}{3}\cdot3\sqrt{2x+1}-2\sqrt{2x+1}=18\)
=>\(9\sqrt{2x+1}=18\)
=>\(2x+1=4\)
=>\(x=\dfrac{3}{2}\left(nhận\right)\)
a:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\3x-2>=0\end{matrix}\right.\Leftrightarrow x>=\dfrac{2}{3}\)
\(\sqrt{x}+\sqrt{3x-2}=2\)
=>\(\left(\sqrt{x}+\sqrt{3x-2}\right)^2=4\)
=>\(x+3x-2+2\sqrt{x\left(3x-2\right)}=4\)
=>\(4x-2+2\sqrt{x\left(3x-2\right)}=4\)
=>\(2\sqrt{x\left(3x-2\right)}=4x-6\)
=>\(\sqrt{3x^2-2x}=2x-3\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\3x^2-2x=4x^2-12x+9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\4x^2-12x+9-3x^2+2x=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x^2-10x+9=0\end{matrix}\right.\Leftrightarrow x=9\)
b: ĐKXĐ: x+1>=0
=>x>=-1
\(2\sqrt{9x+9}-\dfrac{1}{4}\sqrt{16x+16}-5\sqrt{x+1}=-6-\sqrt{4x+4}\)
=>\(6\sqrt{x+1}-\dfrac{1}{4}\cdot4\sqrt{x+1}-5\sqrt{x+1}+\sqrt{4x+4}=-6\)
=>\(6\sqrt{x+1}-\sqrt{x+1}-5\sqrt{x+1}+2\sqrt{x+1}=-6\)
=>\(2\sqrt{x+1}=-6\)(vô lý)
Vậy: Phương trình vô nghiệm