
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


thích làm mỗi bài 10:
\(\left\{\begin{matrix}x+y=45\\8x+9y=379\end{matrix}\right.\)
số hs dc điểm x = 26hs
x = 26 hs9đ



Lời giải:
Lấy điểm $K$ sao cho $AKCB$ là hình bình hành
Khi đó: \(\overrightarrow{AK}=\overrightarrow {BC}\Leftrightarrow \overrightarrow{KA}+\overrightarrow{BC}=\overrightarrow{0}\)
Ta có:
\(|\overrightarrow{MA}+\overrightarrow{BC}|=|\overrightarrow{MA}-\overrightarrow{MB}|\)
\(\Leftrightarrow |\overrightarrow{MK}+\overrightarrow{KA}+\overrightarrow{BC}|=|\overrightarrow {BA}|\)
\(\Leftrightarrow |\overrightarrow{MK}|=|\overrightarrow{BA}|\)
Vậy tập hợp điểm M nằm trên đường tròn tâm $M$ bán kính \(R=AB\)

2n - 3 chia hết cho n+1
=> 2n + 2 - 5 chia hết cho n + 1
Mà 2n+ 2 chia hết cho n + 1
=> 5 chia hết cho n+1
=> n+1 thuộc \(\left\{-1,1,5,-5\right\}\)
=> n thuộc \(\left\{-2,0,4,-6\right\}\)

\(\frac{6\left(x+5\right)}{42}\)- \(\frac{21x}{42}\) >\(\frac{42x}{42}\) - \(\frac{14\left(6+x\right)}{42}\) =>\(\frac{6x+30-21x}{42}\) > \(\frac{42x-84-14x}{42}\) =>\(\frac{30-15x}{42}\) - \(\frac{28x-84}{42}\)>0
=>\(\frac{30-15x-28x+84}{42}\) > 0 => x< \(\frac{72}{43}\)

Lời giải:
Áp dụng BĐT Bunhiacopxky:
\(\left (\frac{1}{a}+\frac{1}{b}\right)(a+b)\geq (1+1)^2\Rightarrow \frac{1}{a}+\frac{1}{b}\geq \frac{4}{a+b}\) (đpcm)
Áp dụng công thức trên (cho tất cả các phần)
a) \(\left\{\begin{matrix} \frac{1}{a}+\frac{1}{b}\geq \frac{4}{a+b}\\ \frac{1}{b}+\frac{1}{c}\geq \frac{4}{b+c}\\ \frac{1}{c}+\frac{1}{a}\geq \frac{4}{a+c}\end{matrix}\right.\) \(\Rightarrow \) cộng theo về, rút gọn: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{2}{a+b}+\frac{2}{b+c}+\frac{2}{c+a}\)
Ta có đpcm.
b) Áp dụng CT: \(\left\{\begin{matrix} \frac{1}{a+b}+\frac{1}{a+c}\geq \frac{4}{a+b+a+c}=\frac{4}{2a+b+c}\\ \frac{1}{b+c}+\frac{1}{a+c}\geq \frac{4}{a+b+2c}\\ \frac{1}{a+b}+\frac{1}{b+c}\geq \frac{4}{a+2b+c}\end{matrix}\right.\)
Cộng theo vế và rút gọn:
\(\Rightarrow \frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\geq 2\left (\frac{1}{a+2b+c}+\frac{1}{2a+b+c}+\frac{1}{a+b+2c}\right)\)
Ta có đpcm.
c) Áp dụng hai phần a và b:
\(\text{VP}\leq \frac{1}{2}\left (\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\leq \frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
\(\Leftrightarrow \text{VP}\leq \frac{4}{4}=1\) (đpcm)
Dấu bằng xảy ra ở tất cả các phần đều là khi \(a=b=c\)




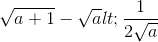 ,a>0
,a>0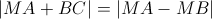
 . Áp dụng chứng minh các BĐT sau:
. Áp dụng chứng minh các BĐT sau:


Ôi giời ơi
sắp loạn thị rồi