
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


11)11) 3x(x-5)2-(x+2)3+2(x-1)3-(2x+1)(4x2-2x+1)=3x(x2-10x+25)-(x3+6x2+12x+8)+2(x3-3x2+3x-1)-(8x3+1)=3x3-30x2+75x-x3-6x2-12x-8+2x3-6x2+6x-2-8x3-1=-4x3-42x2+63x-11


a.\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\);\(ĐK:x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(A=\dfrac{1}{\left(x-1\right)}-\dfrac{2x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x^2+1\right)}\)
\(A=\dfrac{1}{x-1}-\dfrac{2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+1\right)}\)
\(A=\dfrac{x-1}{x^2+1}\)
b.\(A=0,2=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow x^2+1=5x-5\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
c.\(A< 0\) mà \(x^2+1\ge1>0\)
--> A<0 khi \(x-1< 0\)
\(\Leftrightarrow x< 1\)
a. -ĐKXĐ:\(x\ne\pm1\)
\(A=\dfrac{1}{x-1}-\dfrac{x^2+x}{x^2+1}.\left(\dfrac{1}{x-1}-\dfrac{1}{x+1}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\left(\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{\left(x-1\right)\left(x+1\right)}\right)\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{x+1-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{x\left(x+1\right)}{x^2+1}.\dfrac{2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{x^2+1}{\left(x^2+1\right)\left(x-1\right)}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\)
b. \(A=\dfrac{x-1}{x^2+1}=0,2\)
\(\Leftrightarrow\dfrac{x-1}{x^2+1}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{5\left(x-1\right)}{5\left(x^2+1\right)}=\dfrac{x^2+1}{5\left(x^2+1\right)}\)
\(\Rightarrow5x-5=x^2+1\)
\(\Leftrightarrow x^2-5x+1+5=0\)
\(\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=3\left(nhận\right)\end{matrix}\right.\)
c. \(A=\dfrac{x-1}{x^2+1}< 0\)
\(\Leftrightarrow x-1< 0\) (vì \(x^2+1>0\forall x\))
\(\Leftrightarrow x< 1\)

a: Xét tứ giác BFCE có
D là trung điểm của BC
D là trung điểm của FE
Do dó: BFCE là hình bình hành
b: Xét tứ giác ABFE có
AB//FE
AB=FE
Do đó: ABFE là hình bình hành
mà \(\widehat{FAB}=90^0\)
nên ABFE là hình chữ nhật

Bài 4
a) Do Cx // AB
⇒ ∠BCx = ∠ABC = 45⁰ (so le trong)
b) Do AB ⊥ AE
DE ⊥ AE
⇒ AB // DE
Mà Cx // AB
⇒ Cx // DE
c) Do Cx // DE
⇒ ∠DCx = ∠CDE = 60⁰ (so le trong)
⇒ ∠BCD = ∠BCx + ∠DCx
= 45⁰ + 60⁰
= 105⁰

Câu 1
\(a,x-5=3-x\)
\(\Leftrightarrow x+x=3+5\)
\(\Leftrightarrow2x=8\\ \Leftrightarrow x=\dfrac{8}{2}\\ \Leftrightarrow x=4\)
Vậy tập nghiệm của phương trình là \(S=\left\{4\right\}\)
Câu 3:
Xét ΔBAC có MN//AC
nên BN/BC=BM/BA
=>BN/5=2/3
=>BN=15/2=7,5(cm)

\(B=\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
\(B_{min}=-36\) khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(C=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
\(C_{min}=2\) khi \(\left(x;y\right)=\left(1;2\right)\)
b) Ta có: \(B=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\forall x\)
Dấu '=' xảy ra khi x(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy: \(B_{min}=-36\) khi \(x\in\left\{0;-5\right\}\)
c) Ta có: \(C=x^2-2x+y^2-4y+7\)
\(=x^2-2x+1+y^2-4y+4+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy: \(C_{min}=2\) khi (x,y)=(1;2)

Gọi x (tấm) là số thảm được giao của xí nghiệp (x>0)
=> Số tấm thảm xí nghiệp làm được trong 18 ngày là x + 24 ( tấm)
Năng suất dự dịnh: x/20 ( tấm/ngày)
Năng suất thực tế: ( x+24) / 18 (tấm/ngày)
Theo bài ra ta có pt: x/20 + 1/5 * x/20 = (x+24)/18
<=> x = 300
Vậy số tấm thảm xí nghiệp làm trong 18 ngày là 300 + 24 = 324(tấm)

a: Xét tứ giác ABDM có
DM//AB
AM//DB
Do đó: ABDM là hình bình hành
b: Xét ΔCAB và ΔCDB có
CA=CD
BA=BD
CB chung
Do đó: ΔCAB=ΔCDB
Suy ra: \(\widehat{CAB}=\widehat{CDB}=90^0\)
hay BD⊥DC


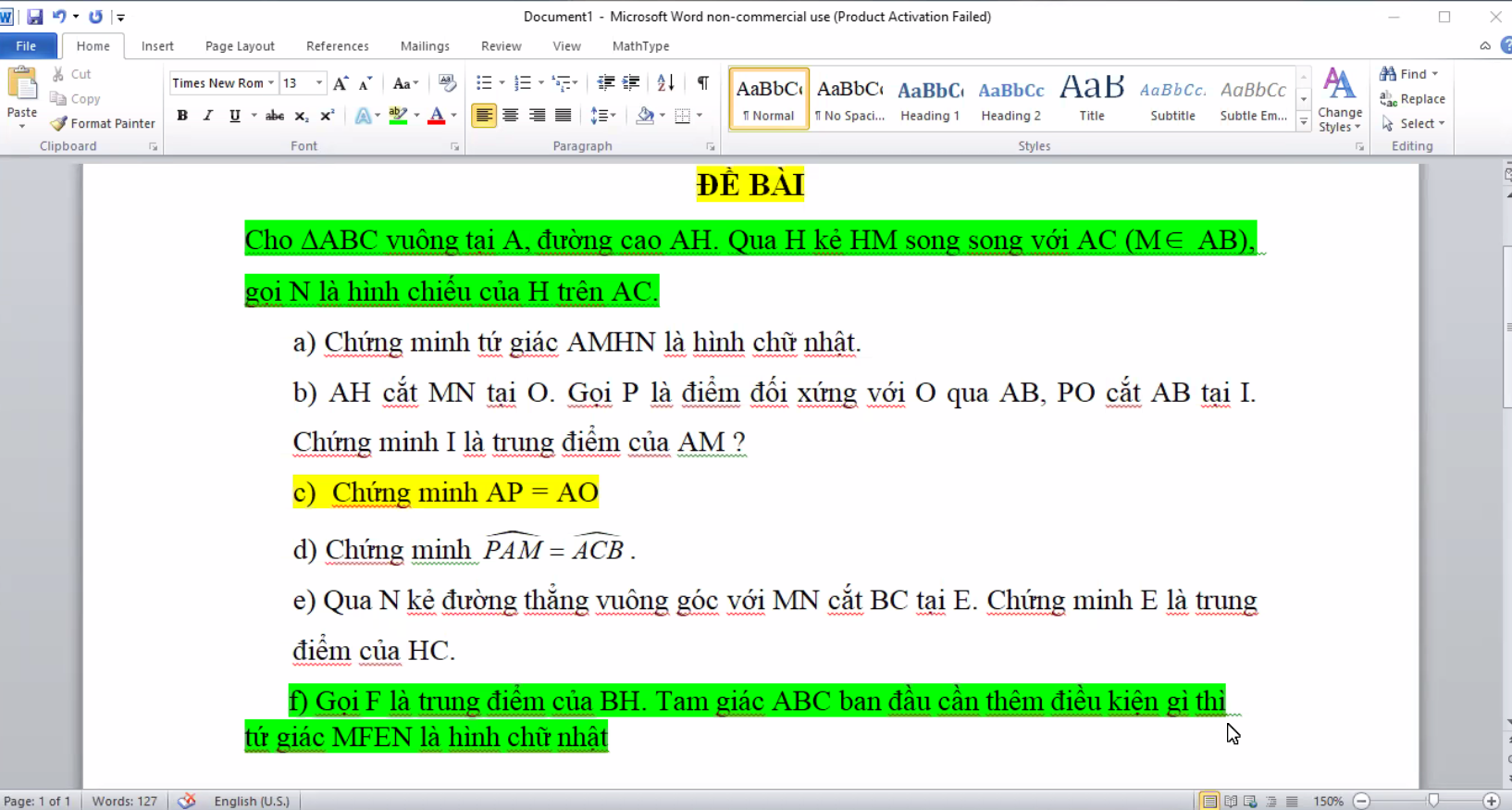
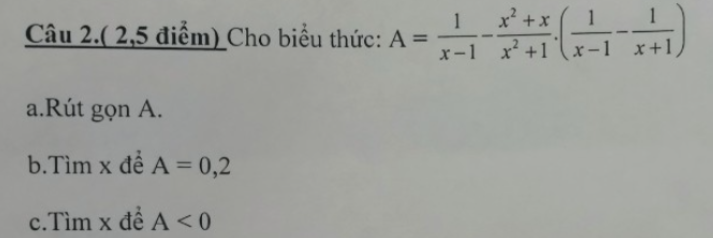

 chi em bai 4 va bai 5 dc ko a em dang can gap a em cam on trc
chi em bai 4 va bai 5 dc ko a em dang can gap a em cam on trc
\(1,P=2x^2-2y^2-x^2+2xy-y^2+x^2+2xy+y^2-4y^2\\ P=2x^2-6y^2+4xy\\ 2,\\ a,=x\left(x-y\right)+3\left(x-y\right)=\left(x+3\right)\left(x-y\right)\\ b,=x\left(x^2-4x-y^2+4\right)\\ =x\left[\left(x-2\right)^2-y^2\right]=x\left(x-y-2\right)\left(x+y-2\right)\\ c,=\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]-3\\ =\left(x^2+5x+4\right)\left(x^2+5x+6\right)-3\\ =\left(x^2+5x+5-1\right)\left(x^2+5x+5+1\right)-3\\ =\left(x^2+5x+5\right)^2-1-3\\ =\left(x^2+5x+5\right)^2-4\\ =\left(x^2+5x+5+2\right)\left(x^2+5x+5-2\right)=\left(x^2+5x+7\right)\left(x^2+5x+3\right)\)
ko co cau 3 ah