Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số phôtôn đến catôt trong 1 s là
\(N = \frac{P}{\varepsilon}= \frac{P\lambda}{hc}= \frac{2.10^{-3}.600.10^{-9}}{6,625.10^{-34}.3.10^8}= 6,04.10^{15}\)
Mà cứ 1000 hạt phô tôn tới ca tôt lại có 2 electron bật ra.
=> Số electron bật ra đến anôt trong 1 s là \(n =\frac{6,04.10^{15}.2}{1000}=1,21.10^{13} \)
=> \(I_{bh}=n|e| = 1,21.10^{13}.1,6.10^{-19}=1,93.10^{-6}A.\)

Công suất của chùm phôtôn là \(P = W.t= 0,3.10^{-3}.1=0,3.10^{-3}W.\)
Số phôtôn đến catôt trong 1 s là \(N =\frac{P}{\varepsilon}=\frac{P\lambda}{hc}= \frac{0,3.10^{-3}.0,2.10^{-6}}{6,625.10^{-34}.3.10^8}= 3,02.10^{14}\)
Số electron bật ra từ catôt đến anôt trong 1 s là \(n = \frac{I_{bh}}{|e|}= \frac{4,5.10^{-6}}{1,6.10^{-19}}= 2,812.10^{13}\)
Hiệu suất lượng tử \(H= \frac{n}{N}.100=\frac{2,812.10^{13}}{.3,02.10^{14}}.100= 9,31 \%\)

Số electron đến anôt trong 1 s là \(n = \frac{I_{bh}}{|e|}= \frac{3.10^{-6}}{1,6.10^{-19}}=1,875.10^{13}. \)
Hiệu suất lượng tử \(H = \frac{n}{N}.100\)=> Số hạt phôtôn bay đến catôt là
\(N = \frac{n.100}{50}= \frac{1,875.10^{13}.100}{50}= 3,75.10^{13}.\)
Công suất của chùm sáng là
\(P = N.\varepsilon = N\frac{hc}{\lambda}=3,75.10^{13}.\frac{6,625.10^{-34}.3.10^8}{0,36.10^{-6}}= 2,07.10^{-5}W= 20,7.10^{-6}W.\)

Số phôtôn đến catôt trong 1 s là \(N = \frac{P}{\varepsilon}= \frac{P\lambda}{hc}= \frac{3.0,35.10^{-6}}{6,625.10^{-34}.3.10^8}= 5,28.10^{18}\)
Số electron bật ra từ catôt đến anôt là \(n =\frac{I_{bh}}{|e|}= \frac{0,02}{1,6.10^{-19}}= 1,25.10^{17}\)
Hiệu suất lượng tử \(H = \frac{n}{N}.100 = \frac{1,25.10^{17}}{5,28.10^{18}}.100 = 2,367 \%\)

Hệ thức Anh -xtanh
\(hf = A+ W_{đ max}\)
=> \(hf = 2,5 +1,5= 4 eV = 4.1,6.10^{-16}J.\)
=> \(\lambda = \frac{hc}{4.1,6.10^{-19}}= \frac{6,625.10^{-34}.3.10^8}{4.1,6.10^{-19}}=0,31 \mu m.\)

- Vì cứ 100 photon tới catôt thì có 1 êlectron bứt ra khỏi catôt nên trong mỗi giây, số êlectron bứt ra khỏi catôt là:
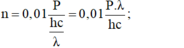
- Khi đó cường độ dòng quang điện bão hòa có giá trị là:
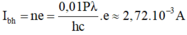


Số phôtôn đến catôt trong 1 s là
\(N = \frac{P}{\varepsilon}= \frac{P\lambda}{hc}= \frac{2.10^{-3}.600.10^{-9}}{6,625.10^{-34}.3.10^8}= 6,04.10^{15}\)
Mà cứ 1000 hạt phô tôn tới ca tôt lại có 2 electron bật ra.
=> Số electron bật ra đến anôt trong 1 s là \(n =\frac{6,04.10^{15}.2}{1000}=1,21.10^{13} \)
=> \(I_{bh}=ne = 1,21.10^{13}.1,6.10^{-19}=1,93.10^{-6}A.\)