Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp:
Công thức liên hệ giữa cường độ dòng điện cực đại và điện tích cực đại: I 0 = ω Q 0
Cách giải:
Điện tích cực đại của tụ là: Q 0 = I 0 ω = 0,04 2.10 7 = 2.10 − 9 C

Đáp án B
Do u và i dao động vuông pha => tại mọi thời điểm ta có:


Đáp án C
Phương pháp: Mạch điện xoay chiều RLC mắc nối tiếp có L thay đổi
Cách giải:
+ Do u L và u C ngược pha nhau => tại mọi thời điểm ta có:
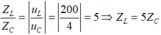
+ Khi L = L 0 thì điện áp hiệu dụng hai đầu cuộn dây đạt cực đại nên:
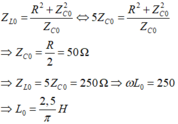

Đáp án A
Phương pháp: Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Cách giải:
Giả sử cuộn dây thuần cảm:
Ta có, khi R = R 2 công suất tiêu thụ trên biến trở cực đại
Khi đó ta có: R 2 = | Z L - Z C | = 40 - 25 = 15 W
Mặt khác: P R 2 = U 2 2 R 2 = 120 2 2.15 = 480 ≠ 160
⇒ điều giả sử ban đầu là sai
⇒ Cuộn dây không thuần cảm có điện trở r
- Ta có:
+ Ban đầu khi mắc vào hai đầu A, M một ắc quy có suất điện động E = 12V, điện trở trong r 1 = 4 W thì I 1 = 0 , 1875
Theo định luật Ôm, ta có: I 1 = E R b + r = E R 1 + r + r 1 → R 1 + r 1 + r = E I 1 = 64 → R 1 + r = 60 Ω ( 1 )
+ Khi mắc vào A,B một hiệu điện thế u = 120 2 cos 100 π t , R = R 2 thì công suất tiêu thụ trên biến trở cực đại và bằng 160W
Ta có:
Công suất trên biến trở R đạt cực đại khi R 2 2 = r 2 + Z L − Z C 2 ( 2 )
Mặt khác, ta có:
Công suất trên R 2 : P = U 2 ( R 2 + r ) 2 + Z L − Z C 2 R 2 = 160 W → R 2 ( R 2 + r ) 2...
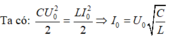

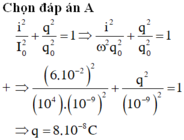
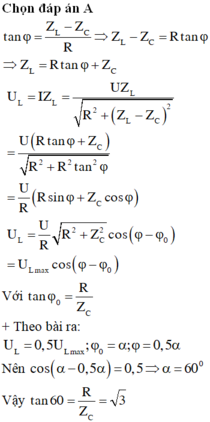

Ta có: \(I_0=\omega.Q_0\)
\(\Rightarrow \omega = \dfrac{I_0}{Q_0}=\dfrac{10}{10^{-6}}=10^7(rad/s)\)
Bước sóng: \(\lambda=c.T=3.10^8.\dfrac{2\pi}{10^7}=60\pi(m)=188,4m\)
Chọn B.
B