Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

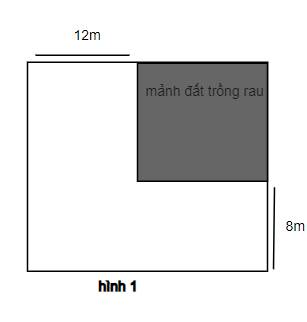
Chiều dài của mảnh đất trồng rau: \(x-8\) (m)
Chiều rộng của mảnh đất trồng rau: \(x-12\left(m\right)\)
Diện tích của mảnh đất trồng rau: \(\left(x-8\right)\left(x-12\right)\left(m^2\right)\)
Ta có phương trình:
\(\left(x-8\right)\left(x-12\right)=96\)
\(\Leftrightarrow x^2-8x-12x+84=96\)
\(\Leftrightarrow x^2-20x+96-96=0\)
\(\Leftrightarrow x^2-20x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=20\left(tm\right)\end{matrix}\right.\)
Vậy độ dài của khu vườn là 20 m

Nếu giả sử chiều rộng của dải hoa = \(w\) mét, thì:
Diện tích một hình chữ nhật ở góc:
\(S_{1} = w \cdot \left(\right. x - w \left.\right)\)
Tổng 4 góc:
\(4 \cdot w \cdot \left(\right. x - w \left.\right) = 60\)
Nếu \(w = 1\) mét
Khi đó:
\(4 \cdot 1 \cdot \left(\right. x - 1 \left.\right) = 60\) \(x - 1 = 15\) \(x = 16 \&\text{nbsp}; \left(\right. \text{m} \overset{ˊ}{\text{e}} \text{t} \left.\right)\)
Nếu mỗi dải hoa rộng 1 mét, cạnh khu vườn là 16 m.
nhé bạn
Giả sử mỗi mảnh đất hình chữ nhật ở góc có một cạnh là \(3\) m, cạnh còn lại bằng \(x\) (chiều cạnh vườn).
Tổng diện tích 4 hình chữ nhật là:
\(4 \times \left(\right. 3 \times x \left.\right) = 60\) \(12 x = 60 \Rightarrow x = 5 \&\text{nbsp};(\text{m})\)
Kết quả:
\(\boxed{x=5\text{m}}\)

Giải:
a, đa thức tính diện tích mảnh đất trồng rau là:
S = \(x.x\) (m2)
S = \(x^2\) (m2)
b,Theo bài ra ta có: \(x^2\) = 96
\(\) \(\left[{}\begin{matrix}x=4\sqrt{6}\\x=-4\sqrt{6}\end{matrix}\right.\)
Vì \(x\) > 0 nên \(x\) = 4\(\sqrt{6}\)
Kết luận: cạnh của khu vườn có độ dài là: 4\(\sqrt{6}\)(m)

a) Q = 3xy(x + 3y) - 2xy(x + 4y) - x²(y - 1) + y²(1 - x) + 36
= 3x²y + 9xy² - 2x²y - 8xy² - x²y + x² + y² - xy² + 36
= (3x²y - 2x²y - x²y) + (9xy² - 8xy² - xy²) + x² + y² + 36
= x² + y² + 36
b) Do x² ≥ 0 với mọi x ∈ R
y² ≥ 0 với mọi x ∈ R
Q = x² + y² + 36 ≥ 36 với mọi x ∈ R
Q nhỏ nhất khi x² + y² = 0
⇒ x = y = 0
Vậy x = y = 0 thì Q nhỏ nhất và giá trị nhỏ nhất của Q là 36
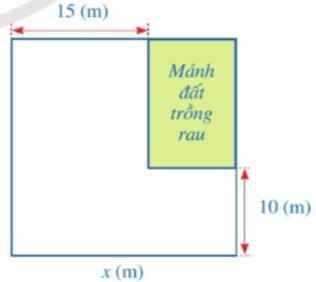
Chiều rộng mảnh đất trồng rau là x-15(m)
Chiều dài mảnh đất trồng rau là x-10(m)
Theo đề, ta có:
(x-15)(x-10)=475
=>\(x^2-25x+150-475=0\)
=>\(x^2-25x-325=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{25+5\sqrt{77}}{2}\left(nhận\right)\\x=\dfrac{25-5\sqrt{77}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy: \(x=\dfrac{25+5\sqrt{77}}{2}\left(m\right)\)