Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có:
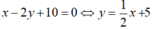
Nên tập nghiệm của phương trình x – 2y + 10 = 0 được biểu diễn bởi đường thẳng (d1):
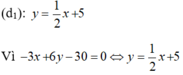
Nên tập nghiệm của phương trình -3x +6y – 30= 0 được biểu diễn bởi đường thẳng (d2):
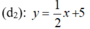
Do đó, nên hệ phương trình đã cho có vô số nghiệm.

Đáp án A
+ Tập nghiệm của phương trình y = 2x + 10 được biểu diễn bởi đường thẳng d 1 :y = 2x + 10.
+ Tập nghiệm của phương trình y = x + 100 được biểu diễn bởi đường thẳng d 2 : y = x + 100.
Lại có: hệ số góc của hai đường thẳng d 1 ; d 2 khác nhau (2 ≠ 1) nên hai đường thẳng này cắt nhau.
Suy ra, hệ phương trình đã cho có nghiệm duy nhất.

1:
a)\(\hept{\begin{cases}nx+x=5
\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x.\left(n+1\right)=5\left(1\right)\\x+y=1\end{cases}}\)

Ta có định lý sau:
Hệ \(\hept{\begin{cases}a_1x+b_1y=c_1\\a_2x+b_2y=c_2\end{cases}}\)
- Có 1 nghiệm duy nhất khi \(\frac{a_1}{a_2}\ne\frac{b_1}{b_2}\)
- Có vô số nghiệm khi \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
Do đó \(\hept{\begin{cases}2x+y=5\\mx-y=-7\end{cases}}\) có 1 nghiệm duy nhất \(\Leftrightarrow\) \(\frac{2}{m}\ne\frac{1}{-1}\) \(\Leftrightarrow\) \(m\ne-2\)
Hệ pt ko thể có vô số nghiệm vì \(\frac{1}{-1}\ne\frac{5}{-7}\)
Đáp án B
Ta có:
Nên tập nghiệm của phương trình – 2x + 5y = 10 được biểu diễn bởi đường thẳng ( d 1 ):
Nên tập nghiệm của phương trình 16x – 40y = 20 được biểu diễn bởi đường thẳng ( d 2 ):
Hai đường thẳng d 1 ; d 2 có cùng hệ số góc và có tung độ góc khác nhau nên d 1 // d 2 .
Suy ra, hệ phương trình đã cho vô nghiệm.