Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
a) \(0,\left(3\right)+3\dfrac{1}{3}+0,4\left(2\right)\)
\(=\dfrac{1}{3}+\dfrac{10}{3}+\dfrac{19}{45}\)
\(=\dfrac{184}{45}\)
b) \(\dfrac{4}{9}+1,2\left(31\right)-0,\left(13\right)\)
\(=\dfrac{4}{9}+\dfrac{1219}{990}-\dfrac{13}{99}\)
\(=\dfrac{1789}{990}\)
Bài 2:
a) \(0,\left(37\right)x=1\)
\(\Leftrightarrow\dfrac{37}{99}.x=1\)
\(\Leftrightarrow x=1:\dfrac{37}{99}\)
\(\Leftrightarrow x=\dfrac{99}{37}\)
b) \(0,\left(26\right)x=1,2\left(31\right)\)
\(\Leftrightarrow\dfrac{26}{99}x=\dfrac{1219}{990}\)
\(\Leftrightarrow x=\dfrac{1219}{990}:\dfrac{26}{99}\)
\(\Leftrightarrow x=\dfrac{1219}{260}\)
Chúc bạn học tốt!
P/s: Mới học trên mạng cái thủ thuật máy tính cầm tay về cái này nên không chắc lắm.Tại mấy bữa nay giờ học máy tính cầm tay trên lớp bị trùng vào ngày học AVTC...=( Có gì sai đừng trách nha.
Ta có:\(45^1\equiv6\left(mod13\right)\)
\(45^2\equiv10\left(mod13\right)\)
....
\(45^5\equiv2\left(mod13\right)\)
Suy ra \(\left(45^5\right)^{200}\equiv2^{200}\left(mod13\right)\)
Tức là \(45^{1000}\) và \(2^{200}\) có cùng số dư khi chia cho 13. (1)
Ta có: \(2^2\equiv4\left(mod13\right)\)
\(2^3\equiv8\left(mod13\right)\)
\(2^4\equiv3\left(mod13\right)\)
......
\(2^8\equiv9\left(mod13\right)\)
.....
\(2^{12}\equiv1\left(mod13\right)\)
Suy ra \(\left(2^{12}\right)^{16}\equiv1^{16}\left(mod13\right)\Leftrightarrow2^{192}\equiv1\left(mod13\right)\)
Suy ra \(2^{192}.2^8\equiv9\left(mod13\right)\Leftrightarrow2^{200}\equiv9\left(mod13\right)\)
Suy ra 2200 và 9 có cùng số dư khi chia cho 13. (2)
Mà 9 : 13 dư 9. (3)
Kết hợp (1);(2);(3) ta có 45100 chia có 13 dư 9.
a: Ta có: \(0,\left(3\right)+\dfrac{10}{3}+0,4\left(2\right)\)
\(=\dfrac{1}{3}+\dfrac{10}{3}+\dfrac{4}{9}\)
\(=\dfrac{33}{9}+\dfrac{4}{9}=\dfrac{37}{9}\)
b: Ta có: \(\dfrac{4}{9}+1.2\left(31\right)-0,\left(13\right)\)
\(=\dfrac{4}{9}+\dfrac{1219}{990}-\dfrac{13}{99}\)
\(=\dfrac{440}{990}+\dfrac{1219}{990}-\dfrac{130}{990}\)
\(=\dfrac{139}{90}\)
c: Ta có: \(2,\left(4\right)\cdot\dfrac{3}{11}\)
\(=\dfrac{22}{9}\cdot\dfrac{3}{11}\)
\(=\dfrac{2}{3}\)
d: Ta có: \(-0,\left(3\right)+\dfrac{1}{3}\)
\(=-\dfrac{1}{3}+\dfrac{1}{3}\)
=0
a) Kết quả trên màn hình là: 5
Suy ra: \({x^2} = {5^2} = 25\)
b) Kết quả trên màn hình là: \(1,41421...\)
Suy ra: \({x^2} = 2\)
(ở một số máy tính nút luỹ thừa còn có dạng 
)
a) \({(3,147)^3} \approx 31,167\)
b) \({( - 23,457)^5} \approx - 7\,101\,700,278\)
c) \({\left( {\frac{4}{{ - 5}}} \right)^4} = \frac{{256}}{{625}}\);
d) \({(0,12)^2} \cdot {\left( {\frac{{ - 13}}{{28}}} \right)^5} \approx - 3,{107.10^{ - 4}}\).
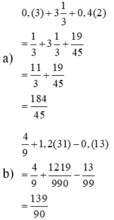
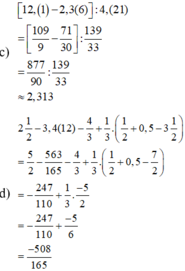
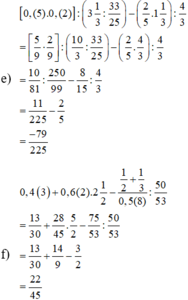
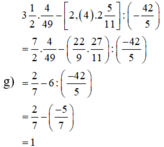
a) \(\dfrac{1}{3}\) + \(\dfrac{7}{2}\) + \(\dfrac{19}{45}\)
= \(\dfrac{30}{90}\) + \(\dfrac{315}{90}\) + \(\dfrac{38}{90}\)
= \(\dfrac{383}{90}\)
b) \(\dfrac{4}{9}\) + 1,2(31) - 0,(13)
= \(\dfrac{4}{9}\) + \(\dfrac{1219}{990}\) - \(\dfrac{13}{99}\)
= \(\dfrac{440}{990}\) + \(\dfrac{1219}{990}\) - \(\dfrac{130}{990}\)
= \(\dfrac{1529}{990}\)
= \(\dfrac{139}{90}\)
\dfrac49 + 1,2(31) - 0,(13)
4
a) 1331 + 7227 + 19454519
= 30909030 + 3159090315 + 38909038
= 3839090383
b) 4994 + 1,2(31) - 0,(13)
= 4994 + 12199909901219 - 13999913
= 440990990440 + 12199909901219 - 130990990130
= 15299909901529
= 1399090139