Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 9:
a: Xét tứ giác OPMN có
góc OPM+góc ONM=180 độ
=>OPMN là tứ giác nội tiếp
b: \(MN=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: ΔOAB cân tại O
mà OH là đường trung tuyến
nên OH vuông góc AB
Xét tứ giác OHNM có
góc OHM=goc ONM=90 độ
=>OHNM là tứ giác nội tiép
=>góc MHN=góc MON

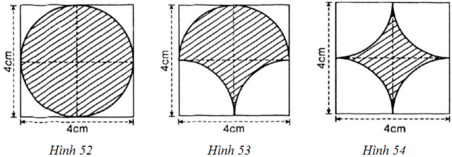
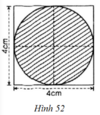
- Hình 52:
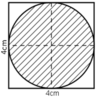
Phần gạch chéo là đường tròn đường kính d = 4cm
⇒ Chu vi của hình là: C = π.d = 4π ≈ 12,57 (cm)
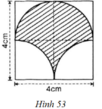
- Hình 53:
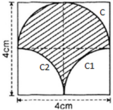
Chu vi gồm nửa đường tròn C; cung tròn C1 và cung tròn C2.
+ C là nửa đường tròn đường kính d = 4cm
⇒ C = π.d/2 = 2π (cm)
+ C1 và C2 là ¼ đường tròn bán kính R = 2cm
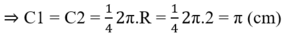
Vậy chu vi phần gạch chéo bằng:
C + C 1 + C 2 = 2 π + π + π = 4 π ≈ 12 , 57 ( c m )
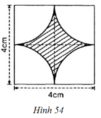
- Hình 54:
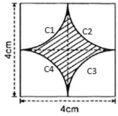
Chu vi cần tính là 4 cung tròn C 1 ; C 2 ; C 3 ; C 4 .
C 1 ; C 2 ; C 3 ; C 4 đều là ¼ đường tròn bán kính R = 2cm.
⇒ C 1 = C 2 = C 3 = C 4
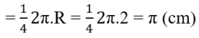
⇒ Chu vi phần hình gạch chéo:
C = C 1 + C 2 + C 3 + C 4 = 4 π ≈ 12 , 57 ( c m ) .
Kiến thức áp dụng
+ Độ dài đường tròn đường kính d là: C = π.d

- Hình 52:
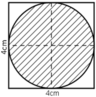
Phần gạch chéo là đường tròn đường kính d = 4cm
⇒ Chu vi của hình là: C = π.d = 4π ≈ 12,57 (cm)
- Hình 53:
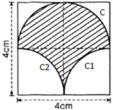
Chu vi gồm nửa đường tròn C; cung tròn C1 và cung tròn C2.
+ C là nửa đường tròn đường kính d = 4cm
⇒ C = π.d/2 = 2π (cm)
+ C1 và C2 là ¼ đường tròn bán kính R = 2cm
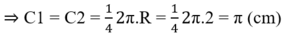
Vậy chu vi phần gạch chéo bằng:
C + C1 + C2 = 2π + π + π = 4π ≈ 12,57 (cm)
- Hình 54:
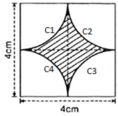
Chu vi cần tính là 4 cung tròn C1 ; C2; C3; C4.
C1 ; C2; C3; C4 đều là ¼ đường tròn bán kính R = 2cm.
⇒ C1 = C2 = C3 = C4
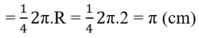
⇒ Chu vi phần hình gạch chéo:
C = C1 + C2 + C3 + C4 = 4π ≈ 12,57 (cm).

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành

a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp


 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ



Mình cảm ơn bạn ạ . Mình thấy lạc quan lên rất nhiều . Chúc bạn có thật nhiều may mắn nhaaa
Hông có j 😊
Cảm ơn bn vì lời chúc nha 😍