Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

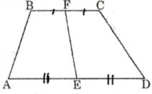
+) Vẽ hình thang ABCD như hình trên. Gọi E, F lần lượt là trung điểm của hai đáy AD BC.
Gọi h là chiều cao của hình thang ABCD. Khi đó h cũng là chiều cao của hình thang BFEA và hình thang FCDE.
+) Diện tích hình thang BFEA là:

+) Lại có: BF = FC (vì F là trung điểm của BC) (3)
AE = DE (vì E là trung điểm của AD) (4)
+) Từ (1); (2); (3) và (4) suy ra: SBFEA = SFCDE.

Cho hình thang ABCD. Gọi M, N lần lượt là trung điểm của hay đáy AB, CD. Ta có hai hình thang AMND và BMNC có cùng chiều cao, có đáy trên bằng nhau AM = MB, có đáy dưới bằng nhau DN = NC. Vậy chúng có diện tích bằng nhau.
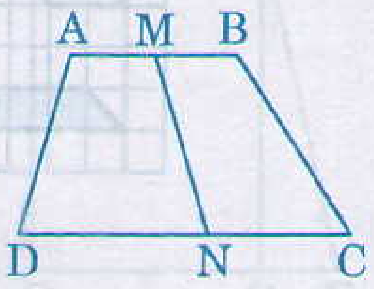


Giả sử hình bình hành ABCD có E, F lần lượt là trung điểm của CD và AB.
Ta có hai hình thang AFED và BFEC có cùng chiều cao, có đáy trên bằng nhau AF = FB, có đáy dưới bằng nhau DE = EC.
=> SAFED = SBFEC


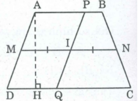
Giả sử hình thang ABCD có AB // CD, đường trung bình là MN. Gọi I là trung điểm của MN, đường thẳng bất kỳ đi qua I cắt AB tại P và CD tại Q.
Ta có hai hình thang APQD và BPQC có cùng đường cao.
MI là đường trung bình của hình thang APQD.
Suy ra: MI = 1/2 (AP + QD)
IN là đường trung bình của hình thang BPQC.
Suy ra: IN = 1/2 (BP + QC)
S A P Q D = 1/2 (AP + QD).AH = MI.AH (1)
S B P Q C = 1/2 (BP + QC).AH = IN.AH (2).
IM = IN (gt) (3)
Từ (1), (2) và (3) suy ra: S A P Q D = S B P Q C , các giá trị này không phụ thuộc vào vị trí của P và Q.

MBA; MCD có : AB//DC => đồng dạng
CD = 3AB => S(MCD) = 32.S(MAB)
S(MCD) = 9.6 = 54 m2
S(ABCD) = S(MCD) - S(MAB) = 54 - 6 = 48 m2

Mình nghĩ rằng bạn bị nhầm đề. Nếu là cạnh AC = 8cm ( có như thế thì mới tìm được liên hệ về độ dài các cạnh là bội số của tam giác vuông) => kq =24 cm2. Cách giải sẽ là: Gọi I, K tương ứng là trung điểm của AD, BC. Lúc đó MIN, MKN là 2 tam giác vuông tại I, K. MINK là hcn. SABCD = 2SMINK= 4SMIN= 24 cm2.
Bạn lầu trên ơi, 2 đường chéo có vuông góc vs nhau đâu mà ta có 2 tam giác vuông đó nhỉ.

