Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(v\left(t\right)=s'\left(t\right)=4.9\cdot2t=9.8t\)
\(a\left(t\right)=v'\left(t\right)=9.8\)
Khi t=3 thì a(3)=9,8

Ta có:
\(\begin{array}{l}h'\left( 2 \right) = \mathop {\lim }\limits_{t \to 2} \frac{{h\left( t \right) - h\left( 2 \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{0,81{t^2} - 0,{{81.2}^2}}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{0,81\left( {{t^2} - {2^2}} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} \frac{{0,81\left( {t - 2} \right)\left( {t + 2} \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} 0,81\left( {t + 2} \right) = 0,81\left( {2 + 2} \right) = 3,24\end{array}\)
Vậy vận tốc tức thời của chuyển động lúc \(t = 2\) là: \(v\left( 2 \right) = h'\left( 2 \right) = 3,24\left( {m/s} \right)\)

a, Quãng đường vật đã rơi tại thời điểm t = 2s sau khi thả vật đó là:
\(s\left(2\right)=0,81\cdot2^2=3,24\left(m\right)\)
b, Ta có: \(s'\left(t\right)=1,62t\Rightarrow s''\left(t\right)=1,62\)
Gia tốc của vật đã rơi tại thời điểm t = 2s sau khi thả vật đó là:
\(a\left(2\right)=s''\left(2\right)=1,62\left(m/s^2\right)\)

Đổi \(200km/h = \frac{{500}}{9}m/s\)
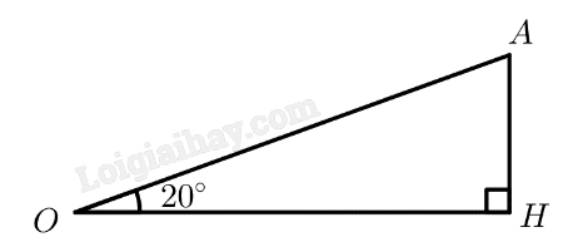
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.

a)
\(\begin{array}{l}\begin{array}{*{20}{l}}{\left[ {5;5,1} \right]}\end{array}:t = 5,1 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{1^2} - 4,{{9.5}^2}}}{{5,1 - 5}} = 49,49\\\begin{array}{*{20}{l}}{\left[ {5;5,05} \right]}\end{array}:t = 5,05 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{05}^2} - 4,{{9.5}^2}}}{{5,05 - 5}} = 49,245\\\begin{array}{*{20}{l}}{\left[ {5;5,01} \right]}\end{array}:t = 5,01 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{01}^2} - 4,{{9.5}^2}}}{{5,01 - 5}} = 49,049\\\begin{array}{*{20}{l}}{\left[ {5;5,001} \right]}\end{array}:t = 5,001 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{001}^2} - 4,{{9.5}^2}}}{{5,001 - 5}} = 49,0049\\\begin{array}{*{20}{l}}{\left[ {4,999;5} \right]}\end{array}:t = 4,999 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{999}^2} - 4,{{9.5}^2}}}{{4,999 - 5}} = 48,9951\\\begin{array}{*{20}{l}}{\left[ {4,99;5} \right]}\end{array}:t = 4,99 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{99}^2} - 4,{{9.5}^2}}}{{4,99 - 5}} = 48,951\end{array}\)

Ta thấy: \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) càng gần 49 khi \(t\) càng gần 5.
b)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,{{9.5}^2}}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - {5^2}} \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - 5} \right)\left( {t + 5} \right)}}{{t - 5}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + 5} \right) = 4,9\left( {5 + 5} \right) = 49\end{array}\)
c)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,9.t_0^2}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - t_0^2} \right)}}{{t - t_0^2}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - {t_0}} \right)\left( {t + {t_0}} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + {t_0}} \right) = 4,9\left( {{t_0} + {t_0}} \right) = 9,8{t_0}\end{array}\)

a)
Vận tốc rơi của viên sỏi lúc `t=2`:
$v(2) = 9,8 \cdot 2 = 19.6 , \text{m/s}$
b)
Khi viên sỏi chạm đất, quãng đường rơi sẽ bằng độ cao ban đầu:
$s(t) = 4.9t^2 = 44.1$
Giải phương trình trên, ta có:
$t^2 = \frac{44.1}{4.9}$
$t \approx 3,0 \text{giây}$
$v(3.0) = 9,8 \cdot 3,0 = 29,4 \text{m/s}$
Vậy vận tốc của viên sỏi khi chạm đất là $29,4 \text{m/s}$.
a: v(t)=s'(t)=4,9*2t=9,8t
Khi t=2 thì v(2)=9,8*2=19,6(m/s)
b: Quãng đường đi được là 44,1m
=>4,9t^2=44,1
=>t=3
Khi t=3 thì v(3)=9,8*3=29,4(m/s)

Chọn A.
Phương pháp:
Ba số x, y, z lập thành một cấp số cộng
⇔ x + z - 2 y
Và số x, y, z lập thành một cấp số nhân ⇔ x z = y 2
Cách giải
Do 3 số x, y, z lập thành một cấp số cộng và có tổng bằng 21 nên ta có
x + z = 2 y x + y + z = 21
⇔ x + z = 14 y = 7
⇔ x = 14 - z y = 7 ( 1 )
Nếu lần lượt thêm các số 2; 3; 9 vào ba số đó (theo thứ tự của cấp số cộng)
thì được ba số lập thành một cấp số nhân nên ta có
( x + 2 ) ( z + 9 ) = ( y + 3 ) 2 ( 2 )
Thay (1) vào (2) ta có:
( 14 - z + 2 ) ( z + 9 ) = ( 7 + 3 ) 2
⇔ z 2 - 7 z - 44 = 0
⇔ z = 11 z = - 4
z = 11 ⇒ z = 14 - 11 = 3
⇒ F = x 2 + y 2 + z 2 = 179
z = - 4 ⇒ x = 14 - ( - 4 ) = 18
⇒ F = x 2 + y 2 + z 2 = 389


a, Ta có:
\(48=16+32\\ 80=48+32\\ 112=80+32\\ 144=112+32\\ ...\)
Vậy dãy số trên là cấp số cộng có số hạng đầu \(u_1=16\) và công sai \(d=32\)
b, Tổng chiều dài quãng đường rơi tự do của người đó trong 10s đầu tiên là:
\(S_{10}=\dfrac{10\cdot\left[u_1+\left(10-1\right)d\right]}{2}=\dfrac{10\cdot\left[2u_1+9d\right]}{2}=\dfrac{10\cdot\left(2\cdot16+9\cdot32\right)}{2}=1600\left(feet\right)\)