Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 30 cm =0,3 m; 1 phút =60s
a,\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{N}{t}}=\dfrac{1}{\dfrac{60}{60}}=1\left(s\right)\)
\(\omega=\dfrac{2\pi}{T}=2\pi\left(\dfrac{rad}{s}\right)\)
b,\(v=\dfrac{2\pi}{T}\cdot r=0,6\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,6\pi\right)^2}{0,3}=1,2\pi^2\left(\dfrac{m}{s^2}\right)\)
c, Đổi 10 cm =0,1m
Khoảng cách từ tâm đến điểm được xét =0,3-0,1=0,2(m)
<Rùi tính tiếp>
\(v'=\dfrac{2\pi}{T}r'=0,4\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}'=\dfrac{v'^2}{r'}=\dfrac{\left(0,4\pi\right)^2}{0,3}=\dfrac{8}{15}\pi^2\left(\dfrac{m}{s^2}\right)\)

Đáp án:
Giải thích các bước giải:
a.
Chu kì là 0,8s
Tần số là:
Tần số góc là:
b.
Tốc độ dài của điểm A là:
c.
Tốc độ dài tại điểm đó là:

Chọn đáp án A
+ Chuyển động tròn đều có tốc độ góc ω không đổI
+ Ta có ![]()
![]()
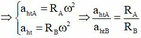
=20/15=4/3

Đổi 40 cm=0,4 m ; 1 phút =60s
Tốc độ dài của điểm A nằm trên vành đĩa
\(v=2\pi\cdot r\cdot f=2\pi\cdot r\cdot\dfrac{N}{t}=2\pi\cdot0,4\cdot\dfrac{30}{60}=0,4\pi\left(\dfrac{m}{s}\right)\)
Gia tốc hướng tâm của điểm A nằm trên vành đĩa
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,4\pi\right)^2}{0,4}=0,4\pi^2\left(\dfrac{m}{s^2}\right)\)
Tốc độ góc của của điểm A nằm trên vành đĩa
\(\omega=\dfrac{v}{r}=\dfrac{0,4\pi}{0,4}=\pi\left(\dfrac{rad}{s}\right)\)

Tần số góc của đĩa tròn là :
\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{0.2}=10\pi\left(\dfrac{rad}{s}\right)\)
Vận tốc dài của một điểm nằm trên vành đĩa là :
\(v=\omega\cdot R=10\pi\cdot0.1=\pi=3.14\left(\dfrac{m}{s}\right)\)

Tốc độ dài: v A = ω r A = 2 π T r A = 2.3 , 14 0 , 75 .0 , 37 = 3 , 1 m/s.
Tốc độ góc: v A = ω r A = 2 π T r A = 2.3 , 14 0 , 75 .0 , 37 = 3 , 1 rad/s.
Gia tốc hướng tâm: a A = v A 2 r A = 3 , 1 2 0 , 37 = 25 , 9 m / s 2 .