Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử sụng hệ thức: 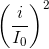 +
+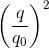 = 1
= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω = 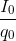 = 50 (rad/s)
= 50 (rad/s)

Khi tăng điện dung nên 2.5 lần thì dung kháng giảm 2.5 lần. Cường độ dòng trễ pha hơn hiệu điện thế $\pi/4$ nên
$Z_L-\frac{Z_C}{2.5}=R$
Trường hợp đầu tiên thì thay đổi C để hiệu điện thế trên C cực đại thì $Z_LZ_C=R^2+Z_L^2$
$Z_LZ_C=(Z_L-\frac{Z_C}{2.5})^2+Z_L^2$
Giải phương trình bậc 2 ta được: $Z_C=\frac{5}{4}Z_L$ hoặc $Z_C=10Z_L$(loại vì Zl-Zc/2.5=R<0)
$R=\frac{Z_L}{2}$
Vẽ giản đồ vecto ta được $U$ vuông góc với $U_{RL}$ còn $U_C$ ứng với cạch huyền
Góc hợp bởi U và I bằng với góc hợp bởi $U_L$ và $U_{LR}$
$\tan\alpha=\frac{R}{Z_L}=0.5$
$\sin\alpha=1/\sqrt5$
$U=U_C\sin\alpha=100V$
\(U_{C}{max}=\frac{U\sqrt{R^{2}+Z_L^{2}}}{R}\); \(Zc=\frac{R^{2}+Z_L^{2}}{Z_L}\)
khi C2=2,5C1---->Zc2=Zc1/2,5=ZC/2,5
do i trể pha hơn U nên Zl>Zc/2,5
\(\tan\frac{\pi }{4}=\frac{Z_L-0,4Zc}{R}=1\Rightarrow R=Z_L-0,4Z_C\)
\(\Rightarrow Z_C.Z_L=Z_L^{2}+(Z_L-0,4Z_C)^{2}\Rightarrow 2Z_L^{2}-1,8Z_CZ_L+0,16Z_C^{2}=0\Rightarrow Z_L=0,8Z_C;Z_L=0,1Z_C\)(loai)
\(\Rightarrow R=Z_L-1,25.0,4Z_L=0,5Z_L\)
\(\Rightarrow U_{C}{max}=\frac{U\sqrt{Z_L^{2}+0,25Z_L^{2}}}{0,5Z_L}=100\sqrt{5}\Rightarrow U=100V\)

Em phải post mỗi câu hỏi 1 bài thôi nhé, để tiện thảo luận.
1. Điều kiện có sóng dừng trên dây có một đầu cố định một đầu tự do: \(L=(2n+1)\frac{\lambda}{4}=(2n+1)\frac{v}{4f}\) (L là chiều dài dây)
\(\Rightarrow n=\frac{1}{2}(\frac{4fL}{v}-1)\)
Do f từ 80Hz đến 120 Hz nên ta tìm được n thỏa mãn sẽ từ 12 đến 17
Do đó có 6 tần số có thể tạo sóng dừng trên dây.
2. Điều chỉnh C để công suất cực đại --> Cộng hưởng xảy ra ---> \(P=\dfrac{U^2}{R}=600(W)\)
Điều chỉnh C = C2 thì công suất sẽ là: \(P_2=\dfrac{U^2}{R}\cos^2(\varphi)=600.(\dfrac{\sqrt 3}{2})^2=450W\)


Xem t = 0 là lúc cả hai mạch bắt đầu dao động
Phương trình hiệu điện thế trên 2 tụ C1 và C2 lần lượt có dạng
\(\begin{cases}u_1=12cos\left(\omega t\right)\left(V\right)\\u_2=6cos\left(\omega t\right)\left(V\right)\end{cases}\)
Độ chênh lệch Hiệu điện thế: \(\Delta u=u_1-u_2=6cos\left(\omega t\right)\left(V\right)\)
\(u_1-u_2=6cos\left(\omega t\right)=\pm3\Rightarrow cos\left(\omega t\right)=\pm0,5\Rightarrow cos\left(\frac{2\pi}{T}t\right)=\pm0,5\)
\(\Rightarrow\Delta t_{min}=\frac{T}{6}=\frac{10^{-6}}{3}s\)

\(f_1 = \frac{1}{2\pi \sqrt{LC_1}}\)
\(f_2 = \frac{1}{2\pi \sqrt{LC_2}}\)
=> \(\frac{f_1}{f_2} = \frac{1}{2}= \sqrt{\frac{C_2}{C_1}} \)=> \(C_1 = 4C_2\)
Mà \(C = \sqrt{C_1C_2} = \sqrt{4C_2C_2} = 2C_2\)
C tăng 2 lần => f giảm \(\sqrt{2}\) lần tức là \(f = \frac{f_2}{\sqrt{2}} = f\sqrt{2}.\)
Chọn đáp án.D

Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)

Tần số dao động riêng: \(f=\frac{1}{2\pi\sqrt{LC}}\Rightarrow\frac{1}{f^2}=k.C\)(Vì chỉ thay đổi C nên ta biểu diễn f theo C, k là một hệ số nào đó)
Suy ra:
\(\frac{1}{f_1^2}=k.C_1\)
\(\frac{1}{f_2^2}=k.C_2\)
Ta cần tìm:
\(\frac{1}{f^2}=k\left(C_1+C_2\right)\Rightarrow\frac{1}{f^2}=kC_1+kC_2\)
\(\Rightarrow\frac{1}{f^2}=\frac{1}{f_1^2}+\frac{1}{f_2^2}\)
Thay số ta đc f = 35Hz

Cường độ dòng điện tức thời qua tụ: \(i=\frac{\Delta q}{\Delta t}=C\frac{\Delta u}{\Delta t}\)
Do 2 tụ mắc song song nên điện áp tức thời 2 đầu mỗi tụ như nhau. Do vậy \(\frac{i_1}{i_2}=\frac{C_1}{C_2}=\frac{1}{2}\Rightarrow i_2=2i_1=2.0,04=0,08A\).
Cường độ dòng điện qua cuộn cảm là: i=i1+i2=0,04+0,08=0,12A
Do năng lượng của tụ: \(W_đ=\frac{1}{2}C.u^2\), nên năng lượng điện tỉ lệ với điện dung C.
Do đó, năng lượng của tụ C1 là: 13,5.10-6 / 2 = 6,75.10-6 (J)
Năng lượng điện của mạch: W = 13,5.10−6+6,75.10-6 =20,25.10-6
Năng lượng điện từ của mạch: \(W=W_đ+W_t=W_{tmax}\Rightarrow 20,25.10^{-6}+\frac{1}{2}.5.10^{-3}.(0,12)^2=\frac{1}{2}.5.10^{-3}.I_0^2\)
=>\(I_0=0,15A\)
Đáp án D

Theo giả thiết: \(Z_C=Z_d=Z=100\)
Suy ra \(Z_C^2=r^2+Z_L^2=r^2+\left(Z_L-Z_C\right)^2=100^2\)
\(\Rightarrow Z_C=2Z_L=100\) \(\Rightarrow\omega^2=\frac{1}{2LC}\) và \(\omega=\frac{50}{L}\)(1)
Lại có: \(\frac{1}{L\left(C-\Delta C\right)}=\left(80\pi\right)^2\Rightarrow LC-L\Delta C=\frac{1}{\left(80\pi\right)^2}\)
Suy ra: \(\frac{1}{2\omega^2}-\frac{50}{\omega}.\frac{0,125.10^{-3}}{\pi}=\frac{1}{80\pi^2}\)
Giải ra ta đc \(\omega=80\pi\)
@phynit: thầy ơi sao tăng thêm một lượng đenta C ta lại lấy C - \(\Delta\)C ạ?
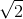
 C1 thì tần số dao động riêng của mạch là f, khi điện dung của tụ là C2
C1 thì tần số dao động riêng của mạch là f, khi điện dung của tụ là C2  thì tần số dao động riêng của mạch là 2f. Khi điện dung của tụ có giá trị bằng
thì tần số dao động riêng của mạch là 2f. Khi điện dung của tụ có giá trị bằng  thì tần số dao động riêng của mạch là
thì tần số dao động riêng của mạch là
Chọn đáp án B