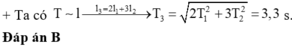Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow l=\dfrac{T\sqrt{g}}{2\pi}\)
Theo đề: \(\left\{{}\begin{matrix}l_3=l_1+l_2\\l_4=l_1-l_2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}l_1=\dfrac{l_3+l_4}{2}\\l_2=\dfrac{l_3-l_4}{2}\end{matrix}\right.\)
Ta có: \(l_1=\dfrac{\sqrt{g}\left(T_3+T_4\right)}{4\pi}=0,8\)
\(l_2=\dfrac{g\left(T_3^2-T_4^2\right)}{8\pi^2}=0,64\)

Đáp án B
+ Ta có T ~ l → l 3 = 2 l 1 + 3 l 2 T 3 = 2 T 1 2 + 3 T 2 2 = 3 , 3

Đáp án C
Phương pháp: Sử dụng công thức tính chu kì của con lắc đơn dao động điều hoà
Cách giải:
Ta có:
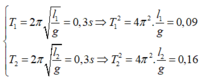
Chu kỳ của con lắc có chiều dài: l3 = l1 + l2 và
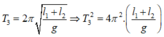
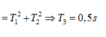

Đáp án D
+ Ta có T = 2 π l g → l = g T 2 π 2 → l 1 = g T 1 2 π 2 l 2 = g T 2 2 π 2
Tương tự như vậy ta cũng có l = l 1 + l 2 = g T 2 π 2
→ T 2 = T 1 2 + T 2 2
+ Nhận thấy rằng T = 2 π l g = 2 π g ⏟ a l hệ số tỉ lệ a trong mối quan hệ tỉ lệ giữ T và l không ảnh hưởng đến kết quả bài toán → Ta có thể giải bài toán này theo một quy trình nhanh hơn. Với T 2 ~ l l = l 1 + l 2
→ T 2 = T 1 2 + T 2 2

\(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow T^2\) tỉ lệ thuận với l
Theo bài ra
\(\left\{{}\begin{matrix}T_1^2+T_2^2=\left(2,7\right)^2=7,29\\T_1^2-T_2^2=\left(0,9\right)^2=0,81\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}T_1^2=4,05\\T_2^2=3,24\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}T_1=2,01s\\T_2=1,8s\end{matrix}\right.\)