Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

$n_{C_2H_2} = \dfrac{6,72}{22,4} = 0,3(mol) ; n_{O_2} = 0,5(mol)$
$2C_2H_2 + 5O_2 \xrightarrow{t^o} 4CO_2 + 2H_2O$
Ta thấy :
$n_{C_2H_2} : 2 > n_{O_2} : 5$ nên $C_2H_2$ dư
Theo PTHH :
$n_{C_2H_2\ pư} = \dfrac{5}{2} = 0,2(mol)$
$n_{CO_2} = 0,4(mol) ; n_{H_2O} = 0,2(mol)$
Suy ra :
$m_{C_2H_2\ dư} = (0,3 - 0,2).26 = 2,6(gam)$
$m_{CO_2} = 0,4.44 = 17,6(gam)$
$m_{H_2O} = 0,2.18 = 3,6(gam)$

\(n_{CO_2}=4a\Rightarrow n_{H_2O}=3a\\ n_{O_2}=0,9mol\\ BT.O:n_{O\left(A\right)}=8a+3a-0,9.2=11a-1,8\left(mol\right)\\ m_A=m_C+m_H+m_O=12.4a+6a+16\left(11a-1,8\right)=17,2\\ a=0,2mol\\ n_C:n_H:n_O=0,8:1,2:0,4=2:3:1\\ CTTN:\left(C_2H_3O\right)_n\\ M_A=43.2=86\\ n\left(12.2+3+16\right)=86\\ n=2\\ A:C_4H_6O_2\)
BT.O:nO(A)=8a+3a−0,9.2=11a−1,8(mol)mA=mC+mH+mO=12.4a+6a+16(11a−1,8)=17,2 giải thích cho mik vs ạ

\(n_{C_2H_2}=\dfrac{2,6}{26}=0,1\left(mol\right)\\ 2C_2H_2+5O_2\rightarrow\left(t^o\right)4CO_2+2H_2O\\ a,n_{O_2}=\dfrac{5}{2}.n_{C_2H_2}=\dfrac{5}{2}.0,1=0,25\left(mol\right)\\ \Rightarrow V_{O_2\left(đktc\right)}=0,25.22,4=5,6\left(l\right)\\ b,n_{CO_2}=\dfrac{4}{2}.n_{C_2H_2}=\dfrac{4}{2}.0,1=0,2\left(mol\right)\\ \Rightarrow m_{CO_2}=0.2.44=8,8\left(g\right)\\ n_{H_2O}=n_{C_2H_2}=0,1\left(mol\right)\\ \Rightarrow m_{H_2O}=0,1.18=1,8\left(g\right)\\ \Rightarrow m_{sp}=m_{CO_2}+m_{H_2O}=8,8+1,8=10,6\left(g\right)\)

\(n_{Mg}=\dfrac{2,4}{24}=0,1mol\)
\(n_{Al}=\dfrac{5,4}{27}=0,2mol\)
\(n_{O_2}=\dfrac{26,88:5}{22,4}=0,24mol\)
\(2Mg+O_2\rightarrow\left(t^o\right)2MgO\)
0,1 0,05 0,1 ( mol )
\(4Al+3O_2\rightarrow\left(t^o\right)2Al_2O_3\)
0,2 0,15 0,1 ( mol )
\(n_{O_2\left(td\right)}=0,05+0,15=0,2mol\)
=> Hỗn hợp A cháy hết
\(\left\{{}\begin{matrix}m_{MgO}=0,05.40=2g\\m_{Al_2O_3}=0,1.102=10,2g\end{matrix}\right.\)

Gọi CTĐGN của A là \(C_xH_y\)
\(n_{CO_2}=\dfrac{4,48}{22,4}=0,2mol\Rightarrow m_C=0,2\cdot12=2,4g\)
\(n_{H_2O}=\dfrac{5,4}{18}=0,3mol\Rightarrow n_H=2n_{H_2O}=0,6mol\Rightarrow m_H=0,6g\)
\(\Rightarrow x:y=n_C:n_H=0,2:0,6=1:3\)
\(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)\(\Rightarrow CTĐGN\) là \(CH_3\)
Gọi CTHH cần tìm là \(\left(CH_3\right)_n\)
Theo bài: \(M_A=15\cdot2=30g\)\(\Rightarrow15n=30\Rightarrow n=2\)
Vậy A cần tìm có CTHH là \(C_2H_6\)
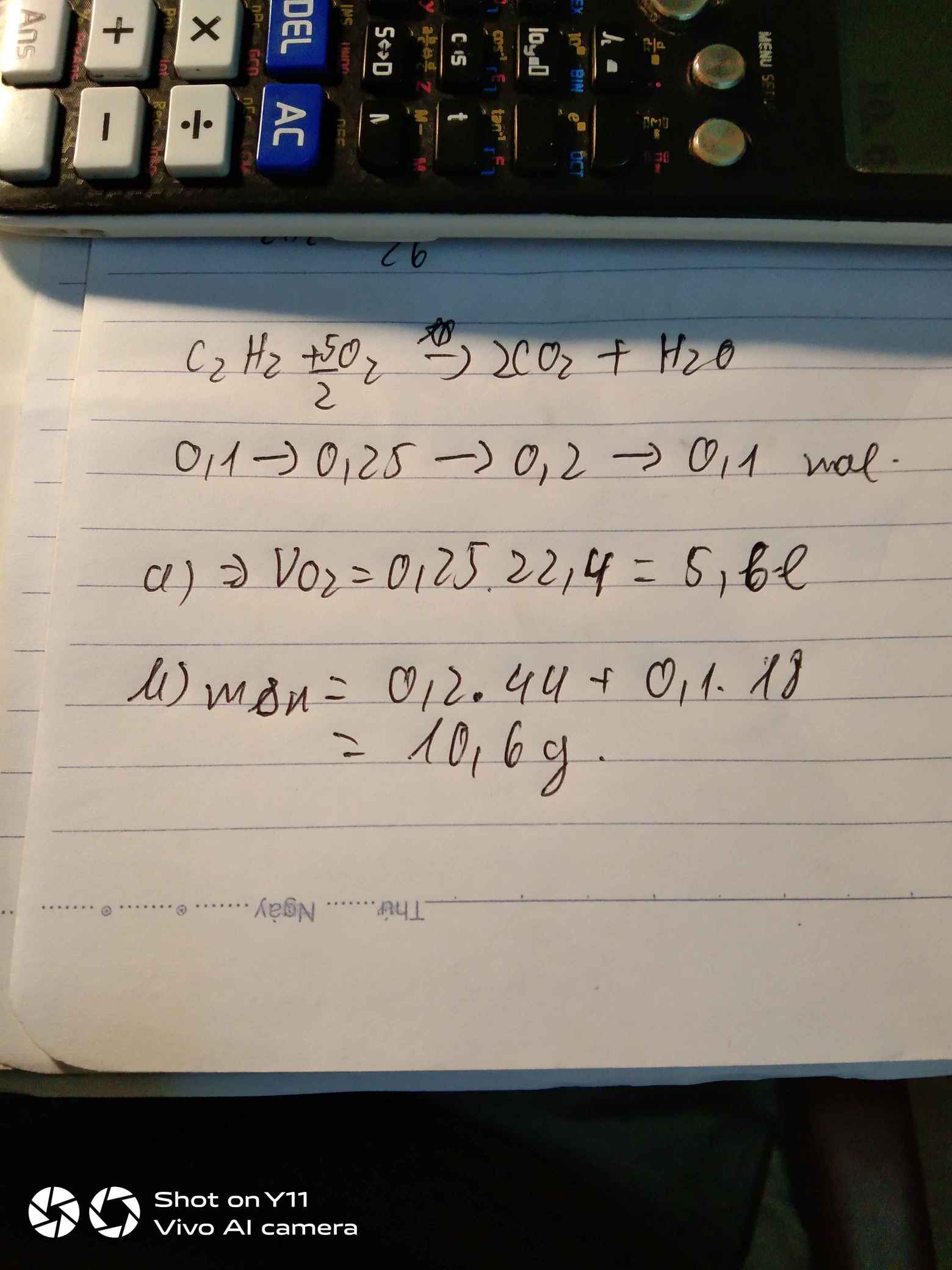
- Chọn câu 1.
C,H và O