Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Công thoát của êlectron ra khỏi bề mặt catôt
\(A=\frac{hc}{\lambda_0}=3,025.10^{-19}J\)
2) Vận tốc ban cực đại của electron
\(V_{max}=\sqrt{\frac{2hc}{m}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)}=5,6.10^5m\text{/}s\)
3) Hiệu điện thế hãm để không có electron về catôt.
\(v_h=\frac{hc}{e}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)=0,91V\)

Đáp án B
+ Ta có λ 1 < λ 2 → ε 1 > ε 2 → v 1 = 1 , 5 v 2 .
+ Áp dụng công thức Einstein về hiệu ứng quang điện cho hai trường hợp ta có:
h c λ 1 = h c λ 0 + E d 1 h c λ 2 = h c λ 0 + E d 2 → h c λ 1 = h c λ 0 + 2 , 25 E d 2 h c λ 2 = h c λ 0 + E d 2 ⇒ 1 , 25 λ 0 = 2 , 25 λ 2 - 1 λ 1
⇔ 1 , 25 λ 0 = 2 , 25 0 , 5 - 1 0 , 4 ⇒ λ 0 = 0 , 625 μ m .

Toàn bộ năng lượng đến trong 1s là:
\(E_1=N_1\frac{hc}{\lambda_1}\)
Năng lượng hạt phát ra trong 1s là :
\(E_2=N_2\frac{hc}{\lambda_2}\)
mặt khác ta có
\(E_2=H.E_1\)
\(N_2\frac{hc}{\lambda_2}=HN_1\frac{hc}{\lambda_1}\)
\(\frac{N_2}{\lambda_2}=H\frac{N_1}{\lambda_1}\)
\(N_2=H\frac{N_1\lambda_2}{\lambda_1}=2.4144.10^{13}hạt\)

Ta có: \(\frac{hc}{\lambda}=A+\frac{1}{2}mv^2_{0max}\left(\text{∗}\right)\)
+Khi chiếu bức xạ có \(\lambda_1:v_{0max1}=\sqrt{\frac{2\left(\frac{hc}{\lambda_1}-A\right)}{m}}\left(1\right)\)
+Khi chiếu bức xạ có \(\lambda_2:v_{0max2}=\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\left(2\right)\)
Từ \(\text{(∗)}\) ta thấy lhi \(\lambda\) lớn thì \(v_{0max}\) nhỏ
\(\Rightarrow v_{0max1}=2,5v_{0max2}\left(\lambda_1<\lambda_2\right)\)
\(\Leftrightarrow\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}=2,5\sqrt{\frac{2\left(\frac{hc}{\lambda_2}-A\right)}{m}}\)
\(\Leftrightarrow\frac{hc}{\lambda_1}-A=6,25\left(\frac{hc}{\lambda_2}-A\right)\) với \(A=\frac{hc}{\lambda_0}\)
\(\Rightarrow\lambda_0=\frac{5,25\lambda_1\lambda_2}{6,25\lambda_1-\lambda_2}=\frac{5,25.0,4.0,6}{6,25.0,4-0.6}=0,663\mu m\)



Đáp án C
Năng lượng mà electron nhận được dùng để thực hiện 3 việc sau:
+ Một phần năng lượng mất mát cho mạng tinh thể để đưa electron lên bề mặt kim loại (nếu electron ở sâu trong kim loại) (Q).
+ Cung cấp cho electron công thoát A để bứt ra khỏi bề mặt kim loại.
+ Cung cấp cho electron một động năng ban đầu ( W d )
Ta có: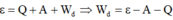
Từ biểu thức trên ta thấy nếu Q=0 (electron ở ngay trên bề mặt kim loại) thì động năng ban đầu W d lớn nhất