Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựa vào đồ thị, ta thấy:
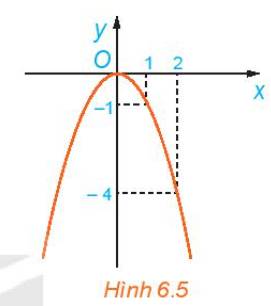
a) Trên khoảng \(\left( { - \infty ;0} \right)\) , giá trị của f(x) tăng
b) Trên khoảng \(\left( {0; + \infty } \right)\) , giá trị của f(x) giảm

Đề bài không đúng em nhé
Đặt \(f\left(\left|x\right|\right)=t\) thì ứng với mỗi giá trị t chỉ cho tối đa 4 nghiệm x
Phương trình trở thành:
\(t-\left(m+1\right)\left|t\right|+m=0\)
\(\Leftrightarrow t-\left|t\right|=m\left(\left|t\right|-1\right)\) (1)
- Với \(t\ge0\) \(\Rightarrow t-t=m\left(t-1\right)\Leftrightarrow m\left(t-1\right)=0\)
+ Với \(m=0\Rightarrow\) pt có vô số nghiệm (ko thỏa mãn)
+ Với \(m\ne0\Rightarrow t=1\Rightarrow f\left(\left|x\right|\right)=1\) có tối đa 4 nghiệm (ktm)
- Với t<0, (1) trở thành:
\(2t=-m\left(t+1\right)\)
Với \(t=-1\) ko phải nghiệm, với \(t\ne-1\) pt trở thành:
\(-m=\dfrac{2t}{t+1}\) (2)
Do \(\dfrac{2t}{t+1}\) đồng biến trên R nên (2) có tối đa 1 nghiệm t
\(\Rightarrow f\left(\left|x\right|\right)=t\) có tối đa 4 nghiệm (ít hơn 8 nghiệm) \(\Rightarrow\) ktm
Do đó không tồn tại m thỏa mãn bài toán

a) 3x^3 -10x+3 =(3x-1)(x-3)
| x | -vc | 1/3 | 5/4 | 3 | +vc | |||||||||
| 3x-1 | - | 0 | + | + | + | + | + | |||||||
| x-3 | - | - | - | - | - | 0 | + | |||||||
| 4x-5 | - | - | - | 0 | + | + | + | |||||||
| VT | - | 0 | + | 0 | - | 0 | + |
Kết luận
VT< 0 {dấu "-"} khi x <1/3 hoắc 5/4<x<3
VT>0 {dấu "+"} khi x 1/3<5/4 hoặc x> 3
VT=0 {không có dấu} khi x={1/3;5/4;3}

\(1.x^2+\dfrac{1}{x^2}-2m\left(x+\dfrac{1}{x}\right)+1+2m=0\left(1\right)\)\(đặt:x^2+\dfrac{1}{x^2}=t\)
\(x>0\Rightarrow t\ge2\sqrt{x^2.\dfrac{1}{x^2}}=2\)
\(x< 0\Rightarrow-t=-x^2+\dfrac{1}{\left(-x^2\right)}\ge2\Rightarrow t\le-2\)
\(\Rightarrow t\in(-\infty;-2]\cup[2;+\infty)\left(2\right)\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2-2mt+2m-1=0\)
\(\Leftrightarrow\left(t-1\right)\left(t-2m+1\right)=0\Leftrightarrow\left[{}\begin{matrix}t=1\notin\left(2\right)\\t=2m-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2m-1\le-2\\2m-1\ge2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m\le-\dfrac{1}{2}\\m\ge\dfrac{3}{4}\end{matrix}\right.\)
\(2.\) \(f^2\left(\left|x\right|\right)+\left(m-2\right)f\left(\left|x\right|\right)+m-3=0\left(1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=3-m\end{matrix}\right.\)
\(dựa\) \(vào\) \(đồ\) \(thị\) \(f\left(\left|x\right|\right)\) \(\Rightarrow f\left(\left|x\right|\right)=-1\) \(có\) \(2nghiem\) \(pb\)
\(\left(1\right)có\) \(6\) \(ngo\) \(pb\Leftrightarrow\left\{{}\begin{matrix}-1< 3-m< 3\\3-m\ne-1\\\end{matrix}\right.\)\(\Leftrightarrow0< m< 4\)
\(\Rightarrow m=\left\{1;2;3\right\}\)