Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\begin{array}{l}a)\frac{{4{\rm{x}} - 6}}{{5{{\rm{x}}^2} - x}}.\frac{{25{{\rm{x}}^2} - 10{\rm{x}} + 1}}{{27 + 8{{\rm{x}}^3}}}\\ = \frac{{ - 2\left( {3 - 2{\rm{x}}} \right)}}{{x\left( {5{\rm{x}} - 1} \right)}}.\frac{{{{\left( {5{\rm{x}} - 1} \right)}^2}}}{{\left( {3 - 2{\rm{x}}} \right)\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\ = \frac{{ - 2\left( {5{\rm{x}} - 1} \right)}}{{x\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\b)\frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}:\frac{{{{\left( {x + 5} \right)}^3}}}{{{x^2} - 9}}\\ = \frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}.\frac{{{x^2} - 9}}{{{{\left( {x + 5} \right)}^2}}}\\ = \frac{{2\left( {x + 5} \right)\left( {x - 3} \right)\left( {x + 3} \right)}}{{{{\left( {x - 3} \right)}^2}{{\left( {x + 5} \right)}^3}}}\\ = \frac{{2\left( {x + 3} \right)}}{{\left( {x - 3} \right){{\left( {x + 5} \right)}^2}}}\end{array}\)

a) Tìm thương và dư (nếu có) trong các phép chia \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right):\left( {3{{\rm{x}}^2}y} \right)\)
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
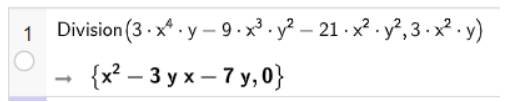
Vậy phép chia hai đa thức \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right)\) cho \(3{{\rm{x}}^2}y\), ta được thương là \({x^2} - 3{\rm{x}}y - 7y\) và dư 0.
b) Tìm thương và dư (nếu có) trong các phép chia (2x3 + 5x2 – 2x + 12) : (2x2 – x + 1).
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

Vậy phép chia hai đa thức (2x3 + 5x2 – 2x + 12) cho (2x2 – x + 1), ta được thương là x + 3 và dư 9.

\(\begin{array}{l}a)\frac{{4{{\rm{x}}^2} - 1}}{{16{{\rm{x}}^2} - 1}}.\left( {\frac{1}{{2{\rm{x}} + 1}} + \frac{1}{{2{\rm{x}} - 1}} + \frac{1}{{1 - 4{{\rm{x}}^2}}}} \right)\\ = \frac{{4{{\rm{x}}^2} - 1}}{{16{{\rm{x}}^2} - 1}}.\frac{{2{\rm{x}} - 1 + 2{\rm{x}} + 1 - 1}}{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}\\ = \frac{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}{{\left( {4{\rm{x}} - 1} \right)\left( {4{\rm{x + 1}}} \right)}}.\frac{{4{\rm{x}} - 1}}{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}\\ = \frac{1}{{4{\rm{x}} + 1}}\\b)\left( {\frac{{x + y}}{{xy}} - \frac{2}{x}} \right).\frac{{{x^3}{y^3}}}{{{x^3} - {y^3}}}\\ = \frac{{x + y - 2y}}{{xy}}.\frac{{{x^3}{y^3}}}{{{x^3} - {y^3}}}\\ = \frac{{\left( {x - y} \right).{x^3}{y^3}}}{{xy\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}} = \frac{{{x^2}{y^2}}}{{{x^2} + xy + y{}^2}}\end{array}\)

a) Phân tích các đa thức \({x^4} - 4{{\rm{x}}^3} - 7{{\rm{x}}^2} + 8{\rm{x}} + 10\)thành nhân tử:
• Sử dụng lệnh Factor(<đa thức>) (hoặc Factorise(<đa thức>)).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
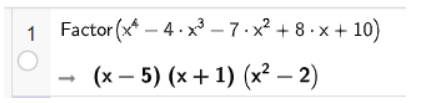
Vậy \({x^4} - 4{{\rm{x}}^3} - 7{{\rm{x}}^2} + 8{\rm{x}} + 10 = \left( {x - 5} \right)\left( {x + 1} \right)\left( {{x^2} - 2} \right)\)
b) Phân tích các đa thức \({\left( {x + y + z} \right)^3} - {x^3} - {y^3} - {z^3}\) thành nhân tử:
• Sử dụng lệnh Factor(<đa thức>) (hoặc Factorise(<đa thức>)).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
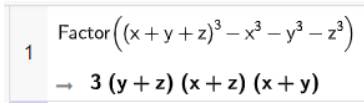
Vậy \({\left( {x + y + z} \right)^3} - {x^3} - {y^3} - {z^3} = 3\left( {y + z} \right)\left( {x + z} \right)\left( {x + y} \right)\)

a) Chỗ sai trong phương trình là: \(5 - x + 8 = 3x + 3x - 27\) (dòng thứ 2) vì khi phá ngoặc đã không đổi dấu của số 8.
Sửa lại:
\(\begin{array}{l}5 - \left( {x + 8} \right) = 3x + 3\left( {x - 9} \right)\\\,\,\,\,5 - x - 8 = 3x + 3x - 27\\\,\,\,\,\,\,\, - 3 - x = 6x - 27\\\,\,\,\, - x - 6x = - 27 + 3\\\,\,\,\,\,\,\,\,\,\,\,\, - 7x = - 24\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \left( { - 24} \right):\left( { - 7} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{{24}}{7}\end{array}\)
Vậy phương trình có nghiệm \(x = \frac{{24}}{7}.\)
b) Chỗ sai trong phương trình là: \(4x + 5x = 9 - 18\) (dòng thứ 3) vì khi chuyển \( - 18\) từ vế trái sang vế phải đã không đổi dấu thành \( + 18\).
Sửa lại:
\(\begin{array}{l}3x - 18 + x = 12 - \left( {5x + 3} \right)\\\,\,\,\,\,\,\,4x - 18 = 12 - 5x - 3\\\,\,\,\,\,\,\,4x + 5x = 9 + 18\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9x = 27\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 27:9\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 3.\end{array}\)
Vậy phương trình có nghiệm \(x = 3.\)

Ta có: \(\begin{array}{l}2{\rm{x}} + 5 = 16\\2{\rm{x}} = 16 - 5\\2{\rm{x}} = 11\\x = \frac{{11}}{2}\end{array}\)
Như vậy, bạn Vuông giải đúng, bạn Tròn giải sai

\(\begin{array}{l}{\left( {a + b} \right)^3} = \left( {a + b} \right){\left( {a + b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a + b} \right)\left( {{a^2} + 2ab + {b^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\; = a.{a^2} + a.2ab + a.{b^2} + b.{a^2} + b.2ab + b.{b^2}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} + 2{a^2}b + a{b^2} + {a^2}b + 2a{b^2} + {b^3}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\end{array}\) \(\begin{array}{l}{\left( {a - b} \right)^3} = \left( {a - b} \right){\left( {a - b} \right)^2}\\\;\;\;\;\;\;\;\;\;\;\; = \left( {a - b} \right)\left( {{a^2} - 2ab + {b^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\; = a.{a^2} - a.2ab + a.{b^2} - b.{a^2} + b.2ab - b.{b^2}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} - 2{a^2}b + a{b^2} - {a^2}b + 2a{b^2} - {b^3}\\\;\;\;\;\;\;\;\;\;\;\; = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\end{array}\)
a) Khai triển biểu thức \({\left( {5{\rm{x}} - y} \right)^2}\)
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
Vậy \({\left( {5{\rm{x}} - y} \right)^2} = 25{{\rm{x}}^2} - 10{\rm{x}}y + {y^2}\)
b) Khai triển biểu thức: \({\left( {\frac{1}{3}x + 2y} \right)^3}\)
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
Vậy \({\left( {\frac{1}{3}x + 2y} \right)^3} = \frac{1}{{27}}{x^3} + \frac{2}{3}{x^2}y + 4{\rm{x}}{y^2} + 8{y^3}\)