với 
là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
chứng minh rằng: 
Chứng minh: 
.
NM
Nguyễn Minh Quang
Giáo viên
26 tháng 2 2021
ta có \(A=\frac{1}{2}+\frac{1}{12}+..>\frac{1}{2}+\frac{1}{12}=\frac{7}{12}\)
\(A=1-\frac{1}{2}+\frac{1}{3}-\left(\frac{1}{4}-\frac{1}{5}\right)-\left(\frac{1}{6}-\frac{1}{7}\right)-..< 1-\frac{1}{2}+\frac{1}{3}=\frac{5}{6}\)
vậy \(\frac{7}{12}< A< \frac{5}{6}\)
b.ta có
\(\frac{6cbx-3acy}{a^2+4b^2}=\frac{6cbx-2abz+2abz-3acy}{a^2+4b^2}=\frac{2bz-3cy}{a}=\frac{3cx-az}{2b}=\frac{ay-2bx}{3c}\)
\(\frac{\Leftrightarrow3c.\left(2bx-ay\right)}{a^2+4b^2}=-\frac{\left(2bx-ay\right)}{3c}\Leftrightarrow\orbr{\begin{cases}2bx-ay=0\\\frac{3c}{a^2+4b^2}=-\frac{1}{3x}\end{cases}}\)phương trình dưới vô nghiệm
vậy \(2bx=ay\Rightarrow2bz-3cy=0\Leftrightarrow\frac{x}{a}=\frac{y}{2a}=\frac{z}{3c}\)
để 
chia hết cho đa thức 
. 
b) 
b) 
HQ
Hà Quang Minh
Giáo viên
12 tháng 1 2024
\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)
21 tháng 4 2017
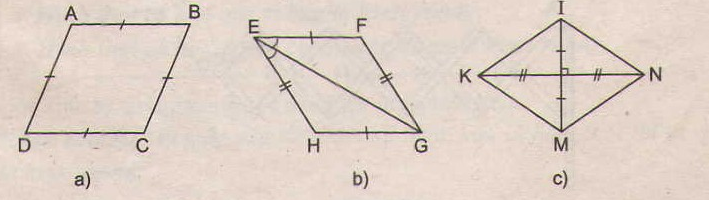
73. Tìm các hình thoi trên hình 102.
Bài giải:
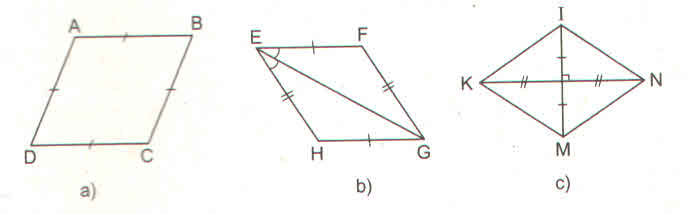
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
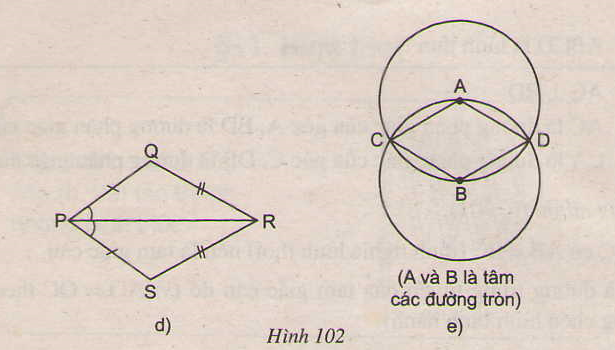
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
21 tháng 4 2017
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
NG
5 tháng 3 2020
Bài 1: Giải phương trình:
a)
b) (x+5)(x+2) – 3(4x-3) = (5 – x) 2
c) ( 3x – 1) 2 – 5( 2x + 1)2 + ( 6x – 3) ( 2x+ 1) = ( x – 1)2
Bài 2: Giải phương trình:
a)
b)
Bài 3: Giải Phương trình với tham số a, b
a) a ( ax+ b) = b2 (x – 1)
b) a2x – ab = b2( x- 1)
Bài 4: Giải phương trình mới tham số a
a)
b)
c)
KN
5 tháng 3 2020
\(\left(x+5\right)\left(x+2\right)-3\left(4x-3\right)=\left(5-x\right)2\)
\(\Leftrightarrow x^2+7x+10-12x+9=10-2x\)
\(\Leftrightarrow x^2-3x+9=0\)
Mà \(x^2-3x+9>0\)nên pt vô nghiệm
H
21 tháng 4 2017
Bài giải:
Ta có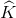 
= 
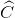= 500 nên IK // BC ( = (đồng vị)
Mà KA = KC suy ra IA = IB = 10cm
Vậy x = 10cm
6 tháng 9 2017
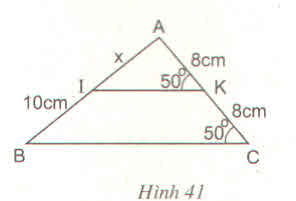
Bài giải:
Ta có \(\widehat{K}\)= \(\widehat{C}\) = 500 nên IK // BC (\(\widehat{K}\) =\(\widehat{C}\) (đồng vị)
Mà KA = KC suy ra IA = IB = 10cm
Vậy x = 10cm
SG
1
10 tháng 5 2017
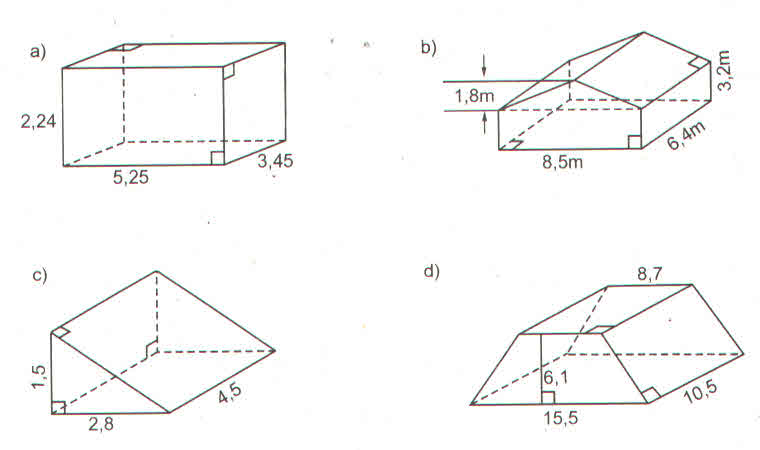
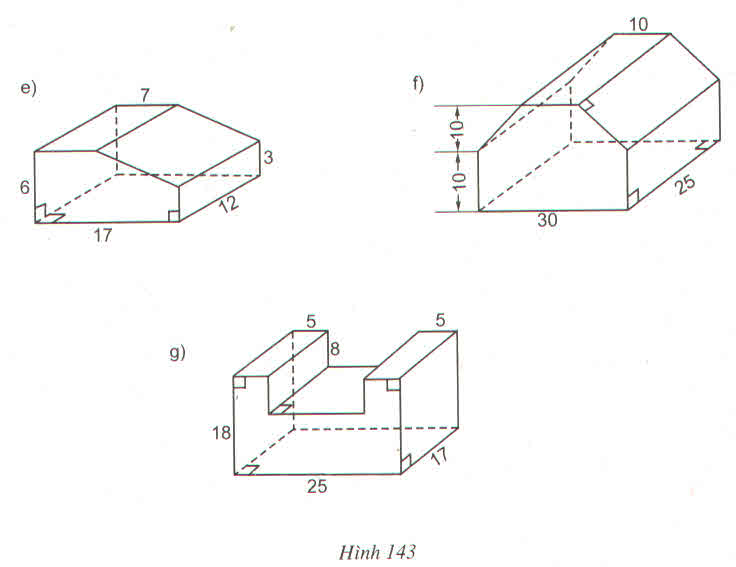
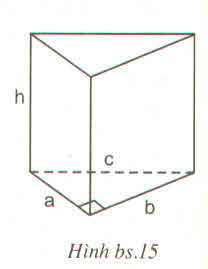
| a | 9 | 35 | 20 | 63 | 28 |
| b | 40 | 12 | 21 | 16 | 45 |
| c | 41 | 37 | 29 | 65 | 53 |
| h | 8 | 18 | 17 | 24 | 13 |
| Diện tích 1 đáy | 180 | 210 | 210 | 504 | 630 |
| Diện tích xung quanh | 720 | 1512 | 1190 | 3456 | 1638 |
| Diện tích toàn phần | 1080 | 1932 | 1610 | 4464 | 2898 |
| Thể tích | 1440 | 3780 | 3570 | 12096 | 8190 |
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
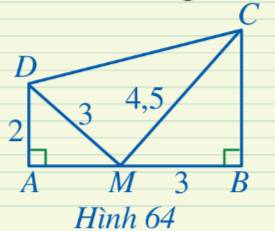
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\) vuông tại \(M\).
D