
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

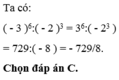

a) \(\left(5x-1\right)^6=729\)
\(\Rightarrow\left[{}\begin{matrix}\left(5x-1\right)^6=3^6\\\left(5x-1\right)^6=\left(-3\right)^6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}5x-1=3\\5x-1=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}5x=4\\5x=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{2}{5}\end{matrix}\right.\)
b) \(\dfrac{8}{25}=\dfrac{2^x}{5^{x-1}}\)
\(\Rightarrow\left[{}\begin{matrix}2^x=2^3\\5^{x-1}=5^2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x-1=2\end{matrix}\right.\)
\(\Rightarrow x=3\)
Vậy x = 3
c) \(\left(\dfrac{1}{16}\right)^x=\left(\dfrac{1}{2}\right)^{10}\)
\(\Rightarrow\left(\dfrac{1}{2}\right)^{3x}=\left(\dfrac{1}{2}\right)^{10}\)
\(\Rightarrow3x=10\)
\(\Rightarrow x=\dfrac{10}{3}\)
d) \(9^x:3^x=3\)
\(\Rightarrow\left(9:3\right)^x=3\)
\(\Rightarrow3^x=3^1\)
\(\Rightarrow x=1\)

\(8< 2^x\le2^9.2^{-5}\)
\(\Leftrightarrow2^3< 2^x\le2^9.\dfrac{1}{2^5}\)
\(\Leftrightarrow2^3< 2^x\le2^4\)
\(\Leftrightarrow x=4\)
Vậy \(x=4\)
\(27< 81^3:3^x< 243\)
\(\Leftrightarrow3^3< \left(3^4\right)^3:3^x< 3^5\)
\(\Leftrightarrow3^3< 3^{12}:3^x< 3^5\)
\(\Leftrightarrow3^3< 3^{12-x}< 3^5\)
\(\Leftrightarrow3^{12-x}=3^4\)
\(\Leftrightarrow12-x=4\)
\(\Leftrightarrow x=4\)
Vậy \(x=4\)

$A=\dfrac{2018.2017-1}{2016.2018+2017}$
$=>A={2018.2016+2018-1}{2016.2018+2017}$
$=>A={2018.2016+2017}{2016.2018+2017}$
$=>A=1$
\(A=\dfrac{2018.2017-1}{2018.2016+2017}\)
\(A=\dfrac{2018.\left(2016+1\right)-1}{2018.2016+2017}\)
\(A=\dfrac{2018.2016+2018-1}{2018.2016+2017}\)
\(A=\dfrac{2018.2016+2017}{2018.2016+2017}=1\)
\(B=\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{1}{27}+\dfrac{1}{81}+\dfrac{1}{243}+\dfrac{1}{729}+\dfrac{1}{2187}\)
\(B=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^7}\)
\(\Rightarrow3B=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^6}\)
\(\Rightarrow3B-B=\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^6}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^7}\right)\)
\(\Rightarrow2B=1-\dfrac{1}{3^7}\Rightarrow B=\dfrac{1-\dfrac{1}{2187}}{2}=\dfrac{1093}{2187}\)
Chúc bạn học tốt!!!

\(\left(a^2+2a+4\right)\left(a-2\right)\\ =\left(a-2\right)\left(a^2+2a+2.2\right)\\ =a^3-8\)
Chọn D
Kết quả của tích (a2+2a+4)(a-2) là
(A) (a+2)3
(B) (a−2)3
(C) a3+8
(D) a3−8

\(\frac{4^x}{2^{x+y}}=8\)
\(\frac{2^{2x}}{2^{x+y}}=2^3\)
\(2x-\left(x+y\right)=3\)
\(x-y=3\)
\(2x-2y=6\)
\(\frac{9^{x+y}}{3^{5y}}=243\)
\(\frac{3^{2x+2y}}{3^{5y}}=3^5\)
\(2x+2y-5y=5\)
\(2x-3y=5\)
mà \(2x-2y=6\)
\(\left(2x-3y\right)-\left(2x-2y\right)=5-6\)
\(-y=-1\)
y = 1
x = 4
Vậy xy = 4

Ta có: \(\left(x^3+8\right)=\left(x+2\right)\left(x^2-2x+4\right)\)
=> \(\left(x^3+8\right):\left(x+2\right)\\ =\left(x+2\right)\left(x^2-2x+4\right):\left(x+2\right)\\ =x^2-2x+4\)
Đáp án: D

Tớ giải được rồi thì có đứa lại nói..... trên mạng có rồi *đau đớn* thế nên có trên mạng rồi thì thôi nha