Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án là A.
• Số phần tử của không gian mẫu là n ( Ω ) = 36 .
Gọi A là biến cố thỏa yêu cầu bài toán.
Phương trình x2 + bx + c = 0 có nghiệm khi và chỉ khi ∆ = b 2 - 4 a c ≥ 0 ⇔ b 2 ≥ 4 a c .
Xét bảng kết quả (L – loại, không thỏa ; N – nhận, thỏa yêu cầu đề bài)
Đáp án B
Phương pháp: Xác suất của biến cố A là n A n Ω trong đó nA là số khả năng mà biến cố A có thể xảy ra, n Ω là tất cả các khả năng có thể xảy ra.
Cách giải: x 2 + b x + c x + 1 = 0 (*)
Để phương trình (*) vô nghiệm thì phương trình x2 + bx + c = 0 (**) có 2 trường hợp xảy ra:
TH1: PT (**) có 1 nghiệm x = -1
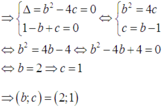
TH2: PT (**) vô nghiệm
Vì c là số chấm xuất hiện ở lần gieo thứ 2 nên c ≤ 6 ⇒ b ≤ 2 6 ≈ 4 , 9 .
Mà b là số chấm xuất hiện ở lần giao đầu nên b ∈ 1 ; 2 ; 3 ; 4
Với b = 1 ta có: c > 1 4 ⇒ c ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 có 6 cách chọn c.
Với b = 2 ta có: c > 1 ⇒ c ∈ 2 ; 3 ; 4 ; 5 ; 6 có 5 cách chọn c.
Với b = 3 ta có: c > 9 4 ⇒ c ∈ 3 ; 4 ; 5 ; 6 có 4 cách chọn c.
Với b = 4 ta có: c > 4 => c ∈ 5 ; 6 có 2 cách chọn c.
Do đó có 6+5+4+2 = 17 cách chọn (b;c) để phương trình (**) vô nghiệm.
Gieo con súc sắc 2 lần nên số phần tử của không gian mẫu n Ω = 6 . 6 = 36
Vậy xác suất đề phương trình (*) vô nghiệm là 1 + 17 36 = 1 2
Đáp án A.
Số phần tử của không gian mẫu là 
Gọi A là biến cố thỏa yêu cầu bài toán.
Phương trình 
có nghiệm khi và chỉ khi
Xét bảng kết quả sau (L – loại, không thỏa; N – nhận, thỏa yêu cầu đề bài):
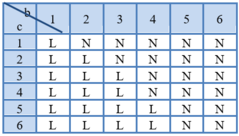
Dựa vào bảng kết quả trên ta thấy số kết quả thuận lợi cho A là 19.
Vậy xác suất của biến cố A là 
.
.
.
.
Đáp án C
Nhắc lại: xác suất của biến cố A được định nghĩa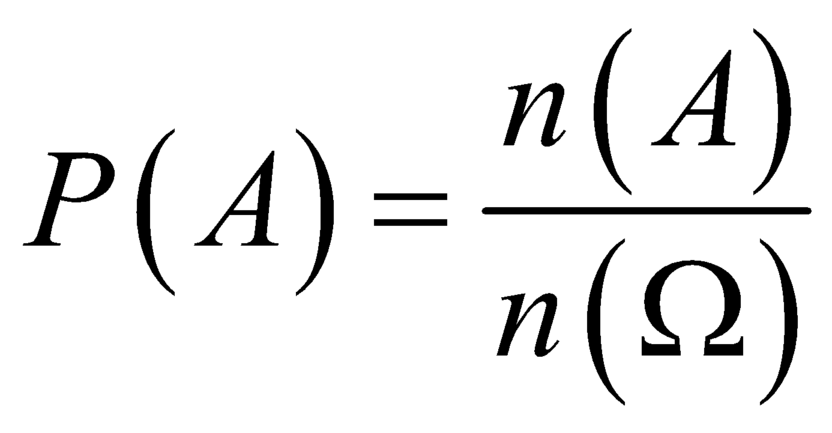 
, với 
là số phần tử của A, 
là số các kết quả có thể xảy ra của phép thử. Số phần tử của không gian mẫu là 
.
Gọi A là biến cố 
, ta có
A={(1;1) ;..(1;6); (2;2);..;(2;6);(3;3);..; (3;6); (4;5); (4;6)}
Suy ra 
. Vậy xác suất để phương trình bậc hai 
vô nghiệm là 17/36.
Chọn C
Số phần tử của không gian mẫu của phép thử gieo một con súc sắc hai lần liên tiếp là 36.
Để phương trình bậc hai
x
2
+ bx + c = 0 có nghiệm là 
(*) với 
Gọi A là biến cố chọn cặp số (b;c) thỏa mãn 
trong đó 
Khi c = 1: Các giá trị của b thỏa mãn điều kiện (*) là: 2,3,4,5,6. Suy ra có: 5 cặp (b,c).
Khi c = 2: Các giá trị của b thỏa mãn điều kiện (*) là: 3,4,5,6. Suy ra có: 4 cặp (b,c).
Khi c = 3: Các giá trị của b thỏa mãn điều kiện (*) là: 4,5,6. Suy ra có: 3 cặp (b,c).
Khi c = 4: Các giá trị của b thỏa mãn điều kiện (*) là: 4,5,6. Suy ra có: 3 cặp (b,c).
Khi c = 5: Các giá trị của b thỏa mãn điều kiện (*) là: 5,6. Suy ra có: 2 cặp (b,c).
Khi c = 6: Các giá trị của b thỏa mãn điều kiện (*) là: 5,6. Suy ra có: 2 cặp (b,c).
Vậy, số cặp (b,c) thỏa mãn điều kiện (*) là 19
Đáp án B
Phương pháp:
Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có nghiệm
⇔ ∆ ≥ 0
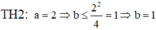
Gọi A là biến cố:
"Phương trình a x 2 + b x + c = 0 có nghiệm"
Không gian mẫu khi gieo con súc sắc cân đối và đồng chất:
Ω = {1, 2, 3, 4, 5, 6}
⇒ n(Ω) = 6
Đặt A: "con súc sắc xuất hiện mặt b chấm";
Xét : x2 + bx + 2 = 0 (1)
Δ = b2 – 8
a. Phương trình (1) có nghiệm
⇔ Δ ≥ 0 ⇔ b ≥ 2√2
⇒ b ∈ {3; 4; 5; 6}.
⇒ A = {3, 4, 5, 6}
⇒ n(A) = 4
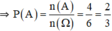
b. (1) vô nghiệm
⇔ Δ < 0 ⇔ b ≤ 2√2
⇒ b ∈ {1; 2}
⇒ A = {1, 2}
⇒ n(A) = 2
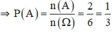
c. phương trình (1) có nghiệm
⇔ b ∈ {3; 4; 5; 6}.
Thử các giá trị của b ta thấy chỉ có b = 3 phương trình cho nghiệm nguyên.
⇒ A = {3}
⇒ n(A) = 1
Không gian mẫu là Ω = {1, 2, 3, 4, 5, 6}. Số kết quả có thế có thể có là 6 (hữu hạn); các kết quả đồng khả năng.
Ta có bảng:
|
b |
1 |
2 |
3 |
4 |
5 |
6 |
|
∆ = b2 - 8 |
-7 |
-4 |
1 |
8 |
17 |
28 |
a) Phương trình x2 + bx + 2 = 0 có nghiệm khi và chỉ khi ∆ = b2 - 8 ≥ 0 (*). Vì vậy nếu A là biến cố: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 có nghiệm"
thì A = {3, 4, 5, 6}, n(A) = 4 và
P(A) = =
.
b) Biến cố B: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 vô nghiệm" là biến cố A, do đó theo qui tắc cộng xác suất ta có
P(B) = 1 - P(A) = .
c) Nếu C là biến cố: "Xuất hiện mặt b chấm sao cho phương trình x2 + bx + 2 = 0 có nghiệm nguyên" thì C = {3}, vì vậy
P(C) = .
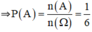
Không gian mẫu Ω = ( b , c ) : 1 ≤ b , c ≤ 6 . Kí hiệu A, B, C là các biến cố cần tìm xác suấtứng với các câu a), b), c). Ta có Δ = b 2 − 4 c
a)
b)
c)