Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C x 1 2 y
a) Ta có: xy//BC
\(\Rightarrow\widehat{A_1}=\widehat{B}\);\(\widehat{A_2}=\widehat{C}\)
b) Vì \(\widehat{A_1}=\widehat{B}\);\(\widehat{A_2}=\widehat{C}\)
=>\(\widehat{A}+\widehat{B}+\widehat{C}=\widehat{A}+\widehat{A_1}+\widehat{A_2}=180^o\)
Chúc bạn học tốt!
Hình bạn Nguyễn Gia Triệu vẽ rồi nha bạn Trần Thị Thu Huyền
a, Các cặp góc bằng nhau:
\(\widehat{A_1}\)và \(\widehat{B}\); \(\widehat{A_2}\)và \(_{\widehat{C}}\)
b, Ta có:
\(\widehat{A_1=\widehat{B};\widehat{A_2}=\widehat{C}}\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=\widehat{A}+\widehat{A_1+\widehat{A_2}=180^o}\)( theo định lý Py-ta-go về tổng ba cạnh tam giác )

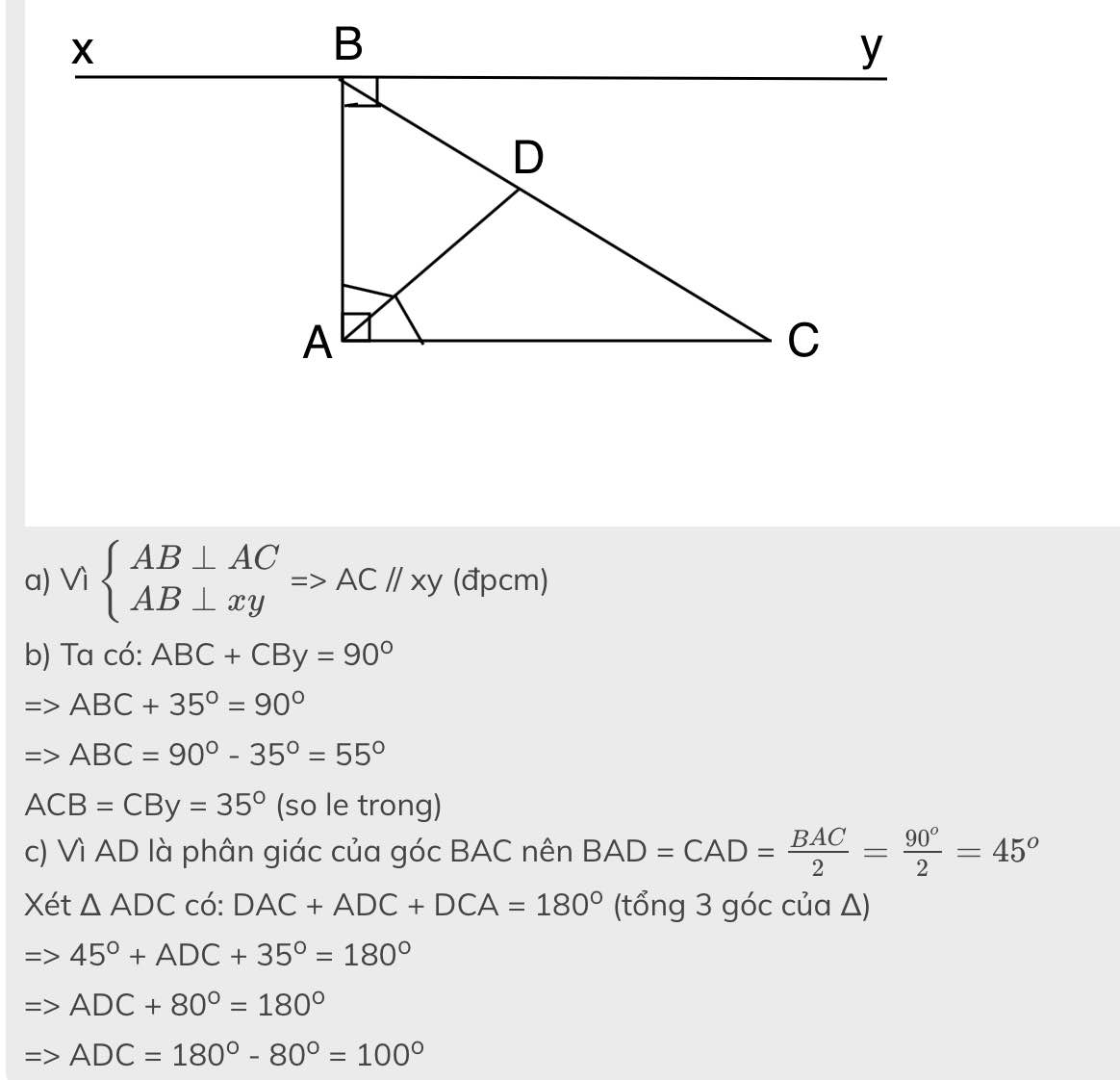
hình tự vẽ bn nha a) ta có:tam giác abc vuông tại a => bac = 90 xét tam giác abc có: abc + acb + cab = 180(t/c) mà bac = 90(cmt) ; acb = 36(gt) => 90 +36 + abc = 180 126 + abc = 180 abc= 54
b) ta có: abd = ebd ( vì bd là phân giác của abc) xét tam giác abd và tam giác ebd có: ba=be(gt) ; abd=ebd(cmt) : chung cạnh bd => tam giác abd = tam giác ebd ( c.g.c) (đpcm)
c) ta có: xy vuông góc với ab(gt) => tam giác abk vuông tại b tam giác abc vuông tại a(gt) => ab vuông góc với ac ta có: xy vuông góc với ab (gt) ab vuông góc với ac(cmt) => xy song song với ac(t/c) => bak = abd ( so le trong) xét tam giác abk vuông tại b và tam giác bad vuông tại a có: bak=abd(cmt) ; chung cạnh ba => tam giác abk= tam giác abd ( cgv-gnk) => ak=bd(2 cạnh tương ứng)

A B C E D 1 2 2 1 1 2 z x y
a, Do DE//BC
=> \(\widehat{A_1}=\widehat{ABC}\)( so le trong )
Vì \(\widehat{BAz}\)là góc ngoài tam giác ABC
=> \(\widehat{BAz}=\widehat{ABC}+\widehat{ACB}\)
\(\Rightarrow\widehat{A_1}+\widehat{A_2}=\widehat{ABC}+\widehat{ACB}\)
Do \(\widehat{A_1}=\widehat{ABC}\)( chứng minh trên )
\(\Rightarrow\widehat{A_2}=\widehat{ACB}\)
Mà góc ABC = góc ACB ( tam giác ABC cân ở A )
=> \(\widehat{A_1}=\widehat{A_2}\)
=> Ax là tia phân giác góc BAz
Hay Ax là phân giác góc ngoài đỉnh A của tam giác ABC
b, Vì \(\widehat{A_2}=\widehat{CAE}\)( 2 góc đối đỉnh)
Mà \(\widehat{A_2}=\widehat{A_1}\)(cmt)
\(\Rightarrow\widehat{A_1}=\widehat{CAE}\)
\(\Rightarrow\widehat{A_1}+\widehat{BAC}=\widehat{CAE}+\widehat{BAC}\)
\(\Rightarrow\widehat{DAC}=\widehat{EAB}\)
Vì góc ABC = góc ACB ( tam giác ABC cân )
=> \(\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{ACB}\Rightarrow\widehat{ABE}=\widehat{ACD}\)
Xét tam giác DAC và tam giác EAB có:
\(\widehat{ACD}=\widehat{ABE}\)( chứng minh trên )
AC = AB ( tam giác ABC cân )
\(\widehat{DAC}=\widehat{EAB}\)( chứng minh trên )
=> \(\Delta DAC=\Delta EAB\)( g-c-g )
=> DA = EA

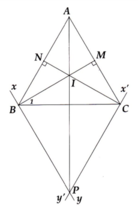
xy//BC
=>\(\widehat{xAB}=\widehat{ABC}\)(hai góc so le trong) và \(\widehat{yAC}=\widehat{ACB}\)(hai góc so le trong)
Ta có: \(\widehat{xAB}+\widehat{BAC}+\widehat{yAC}=180^0\)
=>\(\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\)
=>Tổng số đo 3 góc của ΔABC là 180 độ