K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 8 2021
a: Xét (O) có
\(\widehat{EBF}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{EBF}=90^0\)
Xét (O) có
\(\widehat{EAF}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{EAF}=90^0\)
Xét ΔDEF có
EB là đường cao ứng với cạnh FD
FA là đường cao ứng với cạnh DE
EB cắt FA tại H
Do đó: H là trực tâm của ΔDEF
b: Xét tứ giác DAHB có
\(\widehat{DAH}+\widehat{DBH}=180^0\)
nên DAHB là tứ giác nội tiếp
hay D,A,H,B cùng thuộc 1 đường tròn
25 tháng 8 2021
c: Ta có: I là tâm của đường tròn ngoại tiếp tứ giác DAHB
Suy ra: IA=IB
hay I nằm trên đường trung trực của AB(1)
Ta có: O là tâm đường tròn ngoại tiếp tứ giác ABFE
Suy ra: OA=OB
hay O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OI là đường trung trực của AB
hay OI\(\perp\)AB
d: Điểm K ở đâu vậy bạn?
17 tháng 12 2023
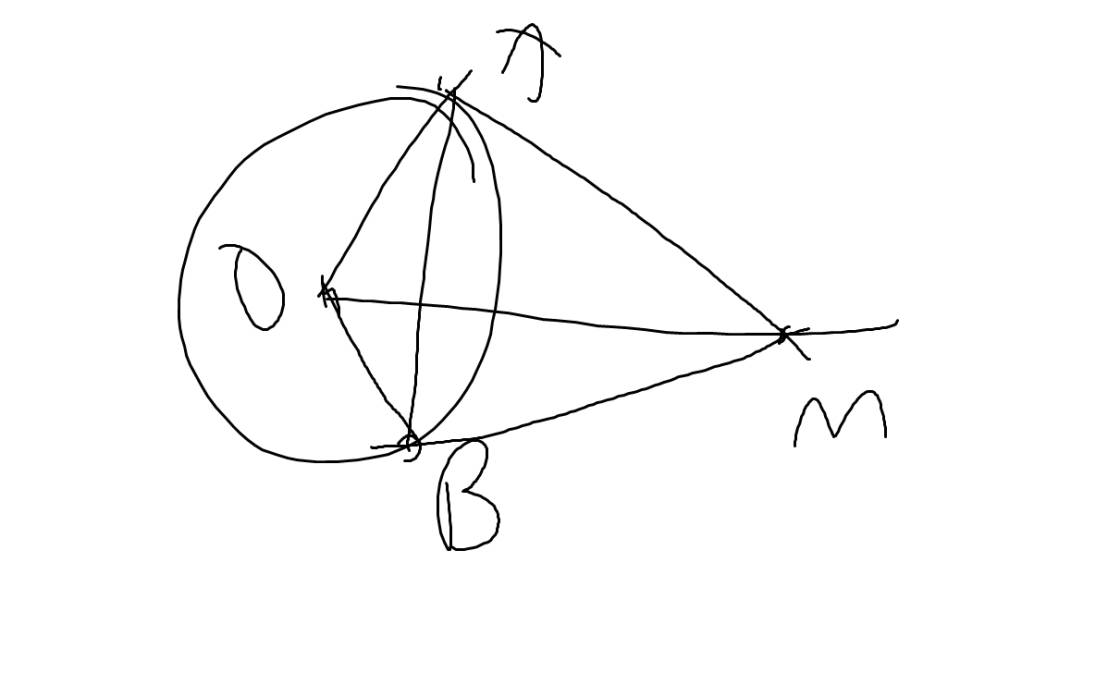
Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
17 tháng 12 2023
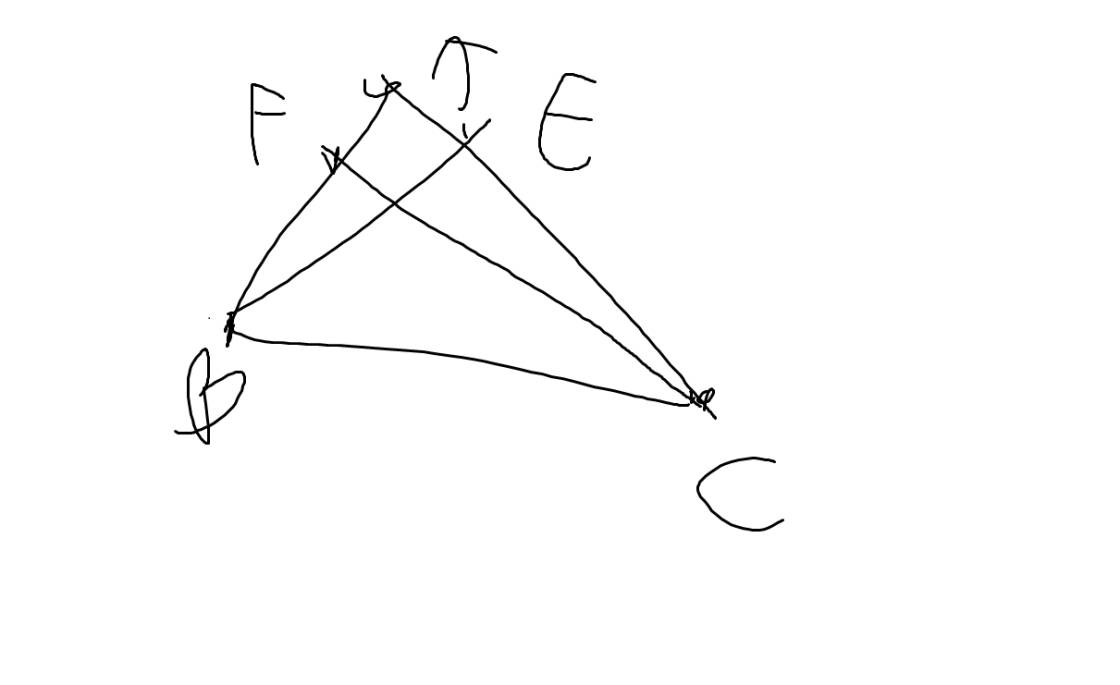
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
giúp kẻ hình nha :'>
28 tháng 11 2023
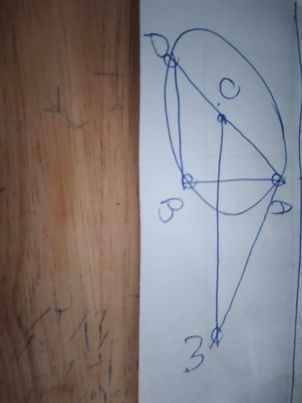
a: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
=>OAMB là tứ giác nội tiếp
=>O,A,M,B cùng thuộc một đường tròn
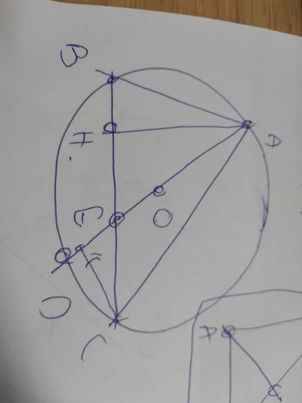
b: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
mà OA=OB
nên OM là đường trung trực của AB
=>OM⊥AB(1)
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó:ΔABD vuông tại B
=>AB⊥BD(2)
Từ (1) và (2) suy ra OM//BD
kẻ hình nx nha
24 tháng 12 2023
a: Xét tứ giác AHKC có \(\widehat{AHC}=\widehat{AKC}=90^0\)
nên AHKC là tứ giác nội tiếp
=>A,H,K,C cùng thuộc một đường tròn
(Cái hình tớ vẽ minh họa thôi nhe, cậu vẽ vào bài làm nhớ căn vuông góc các thứ ha)
Có: `OA = OB = R`
`MA=MB` (tính chất 2 tiếp tuyến cắt nhau tại M)
`=>` `OM` là đường trung trực của `AB`
`=>` `OM \bot AB` tại `H` là trung điểm `AB`.