K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2023
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
22 tháng 3
Đặt \(a = \frac{1}{x} ; b = \frac{1}{y} ; c = \frac{1}{z} \Rightarrow x y z = 1\) và \(x ; y ; z > 0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P = \frac{1}{\frac{1}{x^{3}} \left(\right. \frac{1}{y} + \frac{1}{z} \left.\right)} + \frac{1}{\frac{1}{y^{3}} \left(\right. \frac{1}{z} + \frac{1}{x} \left.\right)} + \frac{1}{\frac{1}{z^{3}} \left(\right. \frac{1}{x} + \frac{1}{y} \left.\right)}\)
\(= \frac{x^{3} y z}{y + z} + \frac{y^{3} z x}{z + x} + \frac{z^{3} x y}{x + y} = \frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}\)
\(P \geq \frac{\left(\left(\right. x + y + z \left.\right)\right)^{2}}{y + z + z + x + x + y} = \frac{x + y + z}{2} \geq \frac{3 \sqrt[3]{x y z}}{2} = \frac{3}{2}\)
\(P_{m i n} = \frac{3}{2}\) khi \(x = y = z = 1\) hay \(a = b = c = 1\)
QT
.png)
1
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
\({x^2} = {4^2} + {2^2} = 20 \Rightarrow x = 2\sqrt 5 \)
\({y^2} = {5^2} - {4^2} = 9 \Leftrightarrow y = 3\)
\({z^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2} = 25 \Rightarrow z = 5\)
\({t^2} = {1^2} + {2^2} = 5 \Rightarrow t = \sqrt 5 \)
LN
1
13 tháng 8
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(HB=HC=\frac{BC}{2}=\frac{12}{2}=6\left(\operatorname{cm}\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=100-36=64=8^2\)
=>HA=8(cm)
b: Diện tích tam giác ABC là:
\(S_{ABC}=\frac12\cdot AH\cdot BC=\frac12\cdot12\cdot8=4\cdot12=48\left(\operatorname{cm}^2\right)\)
LN
5
LN
3
S
subjects
CTVHS
13 tháng 8
a. áp dụnng định lý pythagore vào △ ABC vuông tại A ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(\operatorname{cm}\right)\)
b. diện tích △ ABC là:
\(\frac{6\cdot8}{2}=24\left(\operatorname{cm}^2\right)\)
c. ta có: \(BC\cdot AH=AB\cdot AC\)
\(\Rightarrow AH=\frac{AB\cdot AC}{BC}=\frac{6\cdot8}{10}=4,8\left(\operatorname{cm}\right)\)
áp dụng định lý pythagore vào △ ABH vuông tại H ta được:
\(HB=\sqrt{AB^2-AH^2}=\sqrt{6^2-4,8^2}=3,6\left(\operatorname{cm}\right)\)
áp dụng định lý pythagore vào △ AHC vuông tại H ta được:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{8^2-4,8^2}=6,4\left(\operatorname{cm}\right)\)
d. vì M là trung điểm của cạnh BC
⇒ MB = MC = BC : 2 = 10 : 2 = 5 (cm)
ta có: BH + HM = BM
⇒ HM = BM - BH = 5 - 3,6 = 1,4 (cm)
áp dụng định lý pythagore vào △ AHM vuông tại H ta có:
\(AM=\sqrt{AH^2+HM^2}=\sqrt{4,8^2+1,4^2}=5\left(\operatorname{cm}\right)\)
12 tháng 9
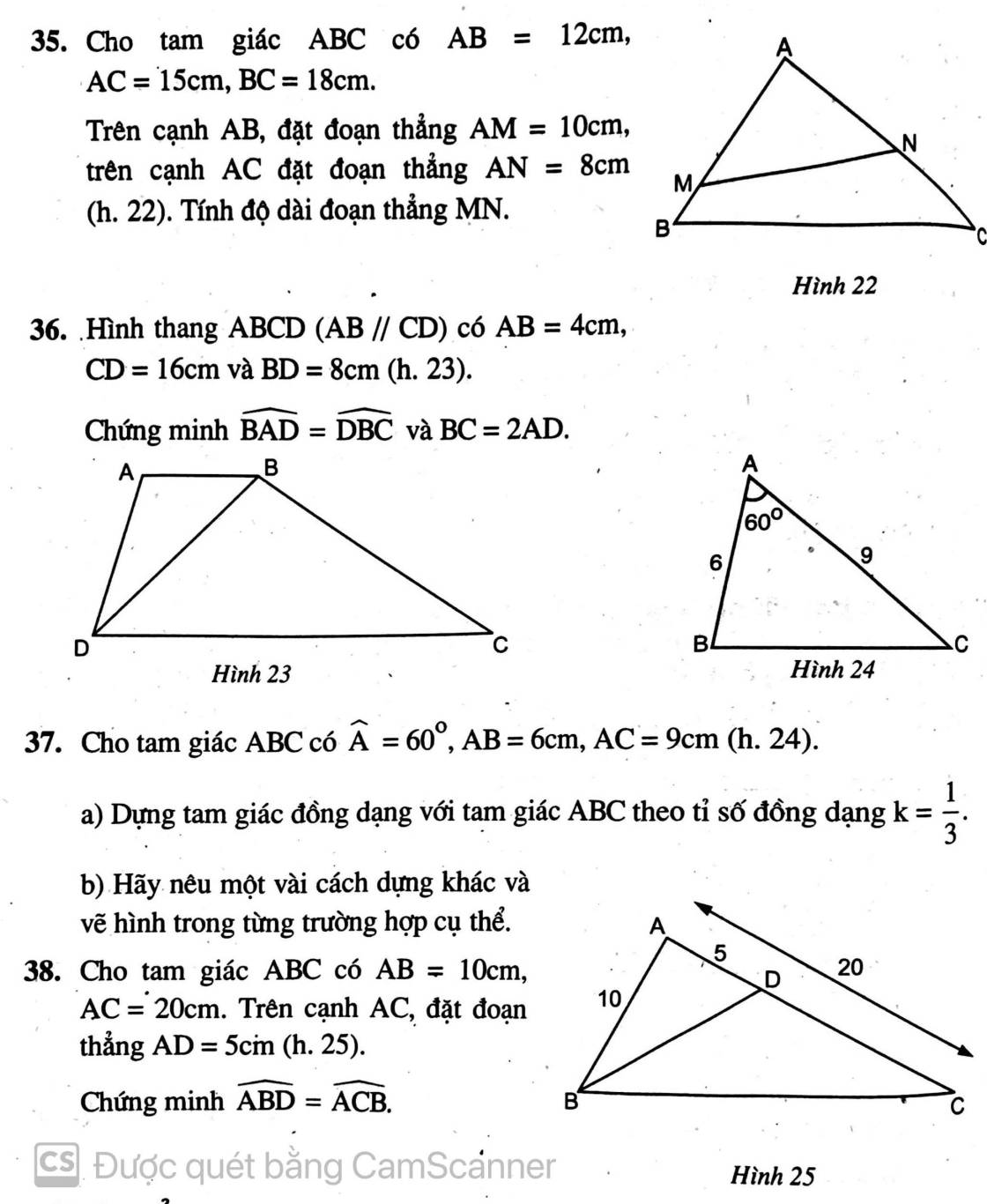
Bài 38:
Xét ΔABD và ΔACB có
\(\frac{AB}{AC}=\frac{AD}{AB}\left(\frac{10}{20}=\frac{5}{10}=\frac12\right)\)
góc BAD chung
Do đó: ΔABD~ΔACB
=>\(\hat{ABD}=\hat{ACB}\)
Bài 36:
Xét ΔABD và ΔBDC có
\(\frac{AB}{BD}=\frac{BD}{DC}\left(\frac48=\frac{8}{16}=\frac12\right)\)
\(\hat{ABD}=\hat{BDC}\) (hai góc so le trong, AB//CD)
Do đó: ΔABD~ΔBDC
=>\(\hat{BAD}=\hat{DBC}\)
ΔABD~ΔBDC
=>\(\frac{AD}{BC}=\frac{AB}{BD}=\frac48=\frac12\)
=>BC=2AD
35:
Xét ΔAMN và ΔACB có
\(\frac{AM}{AC}=\frac{AN}{AB}\left(\frac{10}{15}=\frac{8}{12}=\frac23\right)\)
góc MAN chung
Do đó: ΔAMN~ΔACB
=>\(\frac{MN}{CB}=\frac{AM}{AC}=\frac23\)
=>\(MN=18\cdot\frac23=12\left(\operatorname{cm}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2024
a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)
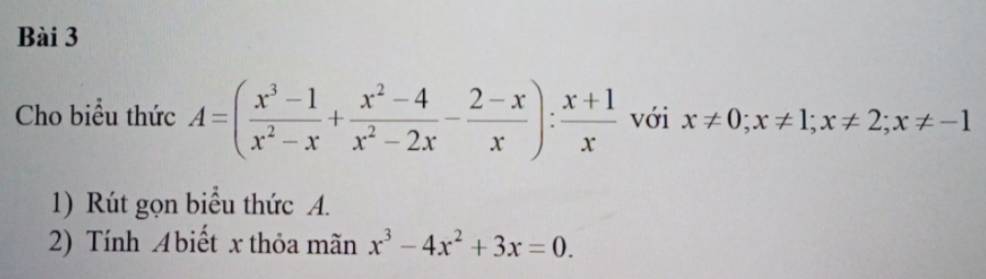
a:
b: AB//CD
=>góc A+góc D=180 độ
mà góc D=2*góc A
nên góc D=2/3*180=120 độ
góc A=180-120=60 độ
AB//CD
=>góc B+góc C=180 độ
mà góc C-góc B=60 độ
nên góc C=(180+60)/2=120 độ và góc B=120-60=60 độ