K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 8 2023
a: 
b: AB//CD
=>góc A+góc D=180 độ
mà góc D=2*góc A
nên góc D=2/3*180=120 độ
góc A=180-120=60 độ
AB//CD
=>góc B+góc C=180 độ
mà góc C-góc B=60 độ
nên góc C=(180+60)/2=120 độ và góc B=120-60=60 độ
13 tháng 1 2022
a: =>3x-2x=-3+2
=>x=-1
bL =>2u+27=4u+27
=>u=0
c: =>5-x+6=12-8x
=>-x+8x=12-6-5=1
=>7x=1
hay x=1/7
7 tháng 7 2023
Xét ΔMAQ vuông tại A và ΔNBP vuông tại B có
MQ=NP
góc Q=góc P
=>ΔMAQ=ΔNBP
=>AQ=BP
=>AQ+AB=BP+BA
=>BQ=AP
24 tháng 11 2019
Cm:Xét tứ tứ giác AEBH có: EM = MH (gt); AM = MB (gt)
\(\widehat{AHB}=90^0\)
=> tứ giác AEBH là hình chữ nhật
=> AE // BH hay AE // BC
b) Xét t/giác ABC cân tại A có AH là đường cao
=> AH cũng là đường trung tuyến
=> BH = HC
Ta có: AEBH là hình chữ nhật => AE = BH
mà BH = HC (cmt)
=> AE = HC
Xét tứ giác ACHE có AE // HC (cmt)
AE = HC (cmt)
=> ACHE là hình bình hành
c) Để hình chữ nhật AHBE là hình vuông
<=> AH = HB
<=> t/giác AHB là t/giác vuông cân
<=> \(\widehat{BAH}=45^0\)
<=> \(\widehat{A}=90^0\) (Do t/giác ABC cân có AH là đường cao => AH là đường trung tuyến)
<=> t/giác ABC vuông cân
Vậy ...
12 tháng 7 2017
Nguyễn Văn Tiến
Cứ mỗi cách chọn 2 đường thẳng thẳng đứng và 2 đường thẳng nằm ngang cho ta 1 hình chữ nhật, suy ra số hình chữ nhật có được là
C26.C25=150 hình chữ nhật
ND
Nguyễn Đức Trí
VIP
31 tháng 7 2023
\(AB^2=AH^2+BH^2\Rightarrow AH^2=AB^2-BH^2\left(1\right)\left(Pitago\right)\)
\(AC^2=AH^2+CH^2\Rightarrow AH^2=AC^2-CH^2\left(2\right)\left(Pitago\right)\)
\(\left(1\right),\left(2\right)\Rightarrow AC^2-CH^2=AB^2-BH^2\)
\(\Rightarrow AB^2+CH^2=AC^2+BH^2\)
\(\Rightarrow dpcm\)
31 tháng 7 2023
Ta có \(AB^2-AC^2=\left(BH^2+AH^2\right)-\left(CH^2+AH^2\right)\) \(=BH^2-CH^2\) \(\Rightarrow AB^2+CH^2=AC^2+BH^2\), đpcm.
(Bài này kết quả vẫn đúng nếu không có điều kiện tam giác ABC vuông tại A.)
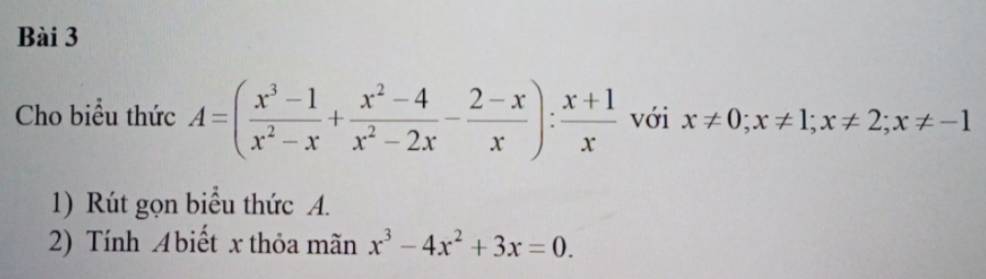
3:
a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
Xét tứ giác BDEC có
DE//BC
góc B=góc C
=>BDEC là hình thang cân
b: góc ABC=góc ACB=(180-góc A)/2
=(180-50)/2=65 độ
=>góc BDE=góc DEC=180-65=115 độ