kẻ cả hình nx 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
kẻ hình nx nha
24 tháng 12 2023
a: Xét tứ giác AHKC có \(\widehat{AHC}=\widehat{AKC}=90^0\)
nên AHKC là tứ giác nội tiếp
=>A,H,K,C cùng thuộc một đường tròn
kẻ hình nx nhé cám ưn nhìu 
7 tháng 12 2023
1: Xét (O) có
ΔAHC nội tiếp
AC là đường kính
Do đó: ΔAHC vuông tại H
=>AH\(\perp\)HC tại H
=>AH\(\perp\)BC tại H
2: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên HM=AM=MB
Xét ΔOAM và ΔOHM có
OA=OH
AM=HM
OM chung
Do đó: ΔOAM=ΔOHM
=>\(\widehat{OAM}=\widehat{OHM}=90^0\)
=>MH là tiếp tuyến của (O)
3: Xét (O) có
\(\widehat{DCH}\) là góc nội tiếp chắn cung DH
\(\widehat{DAH}\) là góc nội tiếp chắn cung DH
Do đó; \(\widehat{DCH}=\widehat{DAH}\)
mà \(\widehat{DAH}=\widehat{DAC}\)(AD là phân giác của góc HAC)
nên \(\widehat{DCH}=\widehat{DAC}\)
Xét ΔDCE và ΔDAC có
\(\widehat{DCE}=\widehat{DAC}\)
\(\widehat{CDE}\) chung
Do đó: ΔDCE đồng dạng với ΔDAC
=>\(\dfrac{DC}{DA}=\dfrac{DE}{DC}\)
=>\(DC^2=DA\cdot DE\)
8 tháng 4 2023
a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH
1 tháng 12 2023
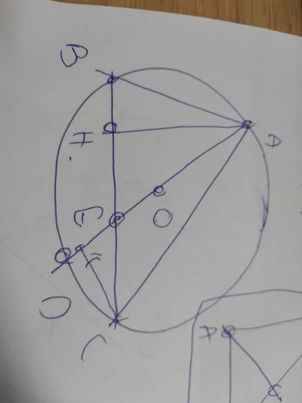
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
HA
0
NP
1
5 tháng 4 2023
a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH
2 tháng 4 2021
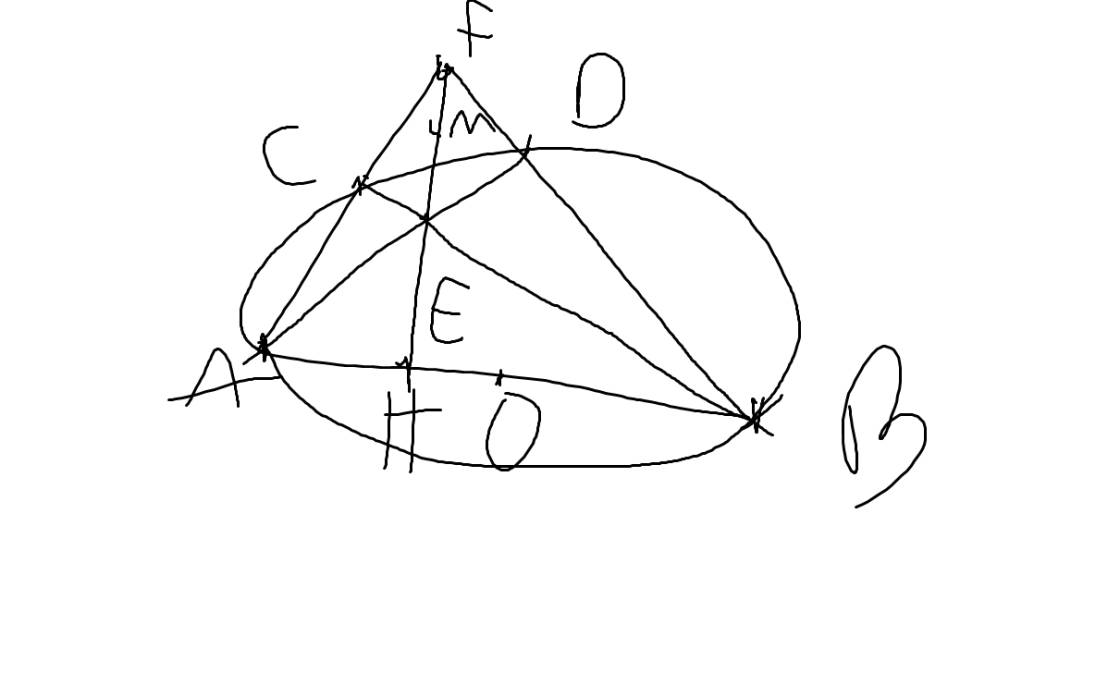
a) Xét (I) có
ΔPMN nội tiếp đường tròn(P,M,N\(\in\)(I))
MN là đường kính(gt)
Do đó: ΔPMN vuông tại P(Định lí)
mà PM=PN(P là điểm chính giữa của (I))
nên ΔPMN vuông cân tại P
\(\Leftrightarrow\widehat{PMN}=45^0\)
hay \(\widehat{SMN}=45^0\)
Xét ΔSNM vuông tại N có \(\widehat{SMN}=45^0\)(cmt)
nên ΔSNM vuông cân tại N(Dấu hiệu nhận biết tam giác vuông cân)
hay NS=NM(Hai cạnh bên)
H
bài 2
giúp mik hai bài này với (kẻ bảng nx nha ) cảm ưn nhiều
1
21 tháng 11 2023
Bài 2:
Gọi khối lượng thóc năm ngoái đơn vị thứ nhất thu hoạch được là x(tấn), đơn vị thứ hai thu hoạch được là y(tấn)
(Điều kiện: x>0 và y>0)
Sản lượng thóc năm nay của đơn vị thứ nhất là: \(x\left(100\%+15\%\right)=1,15x\left(tấn\right)\)
Sản lượng thóc năm nay của đơn vị thứ hai là:
\(y\left(1+12\%\right)=1,12y\left(tấn\right)\)
Tổng sản lượng thóc năm ngoái của hai đơn vị là 720 tấn nên x+y=720(1)
Tổng sản lượng thóc của hai đơn vị năm nay là 819 tấn nên 1,15x+1,12y=819(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=720\\1,15x+1,12y=819\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}1,15x+1,15y=828\\1,15x+1,12y=819\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0,03y=9\\x+y=720\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=300\\x=420\end{matrix}\right.\left(nhận\right)\)
Vậy: Sản lượng thóc năm ngoái của đơn vị thứ nhất là 420 tấn
Sản lượng thóc năm ngoái của đơn vị thứ hai là 300 tấn
Sản lượng thóc năm nay của đơn vị thứ nhất là 420*1,15=483 tấn
Sản lượng thóc năm nay của đơn vị thứ hai là:
300*1,12=336 tấn
a: Xét (O) có
MA,MC là tiếp tuyến
Do đó: MA=MC
=>M nằm trên đường trung trực của AC(1)
OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra MO là đường trung trực của AC
=>MO\(\perp\)AC tại trung điểm của AC
=>MO\(\perp\)AC tại H và H là trung điểm của AC
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó:ΔADB vuông tại D
=>AD\(\perp\)DB tại D
=>AD\(\perp\)BM tại D
Xét ΔMAB vuông tại A có AD là đường cao
nên \(BD\cdot BM=BA^2=4R^2\)
c: Xét ΔOAM vuông tại A có AH làđường cao
nên \(AH^2=OH\cdot HM\)
=>\(4\cdot HO\cdot HM=4\cdot AH^2=AC^2\)
d: Xét ΔMAB vuông tại A có AD là đường cao
nên \(MD\cdot MB=MA^2\)
=>\(MD\cdot MB=MC^2\)