K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
24 tháng 7 2015
làm sao tìm đc:
|3x + 9 - 17| > 0
nên |3x + 9 - 17| ko thể bằng -50
=> x thuộc rỗng
CN
2
1 tháng 2 2018
(x−3)(x2+3x+9)−(3x−17)=x3−12(x−3)(x2+3x+9)−(3x−17)=x3−12
⇒x(x2+3x+9)−3(x2+3x+9)−3x+17=x3−12⇒x(x2+3x+9)−3(x2+3x+9)−3x+17=x3−12
⇒x3+3x2+9x−3x2−9x−27−3x+17=x3−12⇒x3+3x2+9x−3x2−9x−27−3x+17=x3−12
⇒x3+(3x2−3x2)+(9x−9x)−3x−10=x3+12⇒x3+(3x2−3x2)+(9x−9x)−3x−10=x3+12
⇒x3−3x−10=x3+12⇒x3−3x−10=x3+12
⇒x3−3x−10−12=x3⇒x3−3x−10−12=x3
⇒x3−3x−22=x3⇒x3−3x−22=x3
⇒3x−22=0⇒3x−22=0
⇒3x=22⇒x=223
1 tháng 2 2018
(x−3)(x^2+3x+9)−(3x−17)=x^3−12
⇔x^3−27−3x+17=x^3−12
⇔−10−3x=−12
⇔3x=2
⇔x=2/3
Vậy...
PT
4
1 tháng 1 2018
\(\left(\dfrac{1}{3}\right)^{50}.\left(-9\right)^{25}-\dfrac{2}{3}:4\)
=\(\left(\dfrac{1}{9}\right)^{25}.\left(-9\right)^{25}-\dfrac{1}{6}\)
=\(\left[\dfrac{1}{9}.\left(-9\right)\right]^{25}-\dfrac{1}{6}\)
= \(\left(-1\right)^{25}-\dfrac{1}{6}\)
= \(-1-\dfrac{1}{6}=\dfrac{-7}{6}\)
LD
1 tháng 1 2018
\(\left(\dfrac{1}{3}\right)^{50}\cdot\left(-9\right)^{25}-\dfrac{2}{3}:4\)
\(=\left[\left(\dfrac{1}{3}\right)^2\right]^{25}\cdot\left(-9\right)^{25}-\dfrac{1}{6}\)
\(=\left(\dfrac{1}{9}\right)^{25}\cdot\left(-9\right)^{25}-\dfrac{1}{6}\)
\(=\left[\dfrac{1}{9}\cdot\left(-9\right)\right]^{25}-\dfrac{1}{6}\)
\(=\left(-1\right)^{25}-\dfrac{1}{6}=-1-\dfrac{1}{6}=-\dfrac{7}{6}\)
TP
2
22 tháng 2 2016
<=> x - 3x + 17 = 9
<=> - 2x + 17 = 9
<=> - 2x = 9 - 17
<=> - 2x = - 8
=> x = - 8 : ( - 2 )
=> x = 4
Vậy x = 4
26 tháng 6 2022
\(D=\dfrac{9x^8y^6\cdot\dfrac{1}{6}x^2y+\left(-16\right)}{15x^2y^2\cdot0.4\cdot ax^2y^2z^2}=\dfrac{\dfrac{3}{2}x^{10}y^7-16}{6ax^4y^4z^2}\)
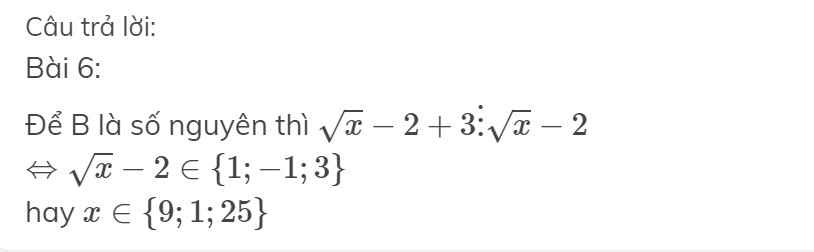
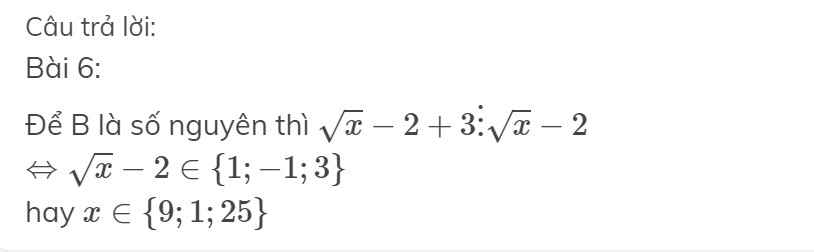
làm sao tìm đc:
|3x + 9 - 17| > 0
nên |3x + 9 - 17| ko thể bằng -50
=> x thuộc rỗng