K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HM
0
PT
1
CM
4 tháng 2 2019
y = - x + 2 x + 2
+) Tập xác định: D = R\{-2}
+) Ta có: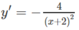 
Bảng biến thiên:
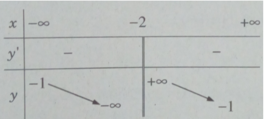
Hàm số nghịch biến trên các khoảng (− ∞ ; −2), (−2; + ∞ )
+) Tiệm cận đứng x = -2 vì
Tiệm cận ngang y = -1 vì
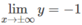
Giao với các trục tọa độ: (0; 1); (2; 0)
Đồ thị
CM
5 tháng 3 2018
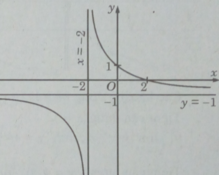
Với m = 2 ta có hàm số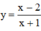 
- Tập xác định : D = R\{-1}.
- Sự biến thiên :
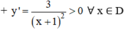
⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).
+ Cực trị : hàm số không có cực trị
+ Tiệm cận :
⇒ y = 1 là tiệm cận ngang của đồ thị hàm số
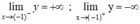
⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên :
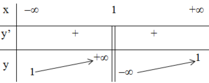
- Đồ thị :
CM
22 tháng 6 2019
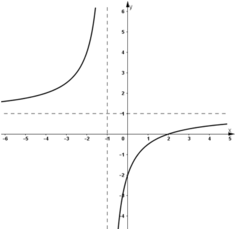
Khi a = 3/2 thì
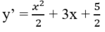
y' = 0 ⇔ x 2 + 6x + 5 = 0 ⇔ x = -1 hoặc x = -5.
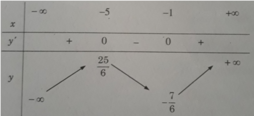
Đồ thị như trên Hình 1.18
Vì
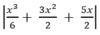
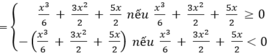
nên từ đồ thị (C) ta suy ngay ra đồ thị của hàm số
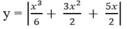
như trên Hình 1.19
PV
0
PT
1
CM
5 tháng 11 2018
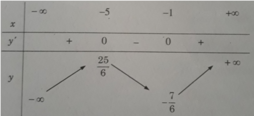
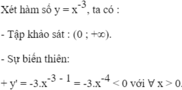
Do đó, hàm số đã cho nghịch biến trên tập xác định.
+ Giới hạn:
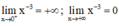
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số
y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
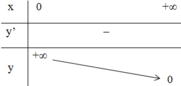
- Đồ thị:
PT
1
CM
22 tháng 3 2017
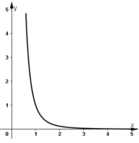
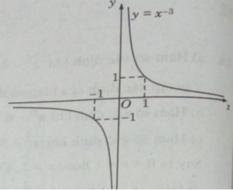
Tập xác định: R\{0}
Hàm số đã cho là hàm số lẻ.
Ta có: y′ < 0, ∀ x ∈ R \ {0} nên hàm số luôn nghịch biến trên các khoảng xác định.
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên:
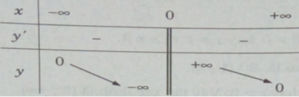
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.
