
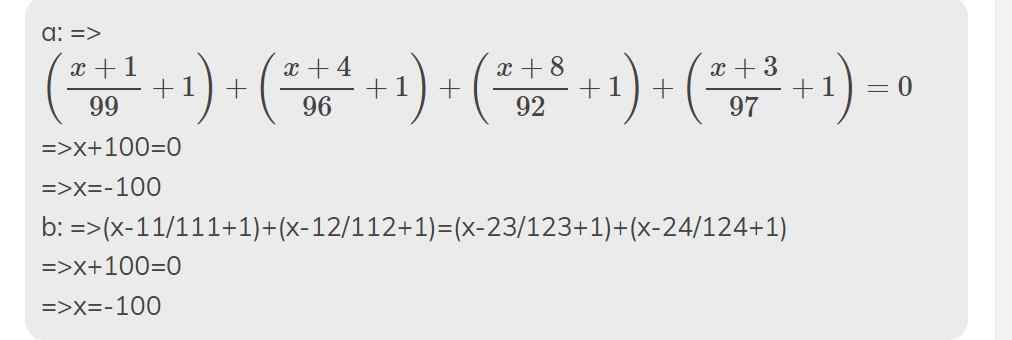
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

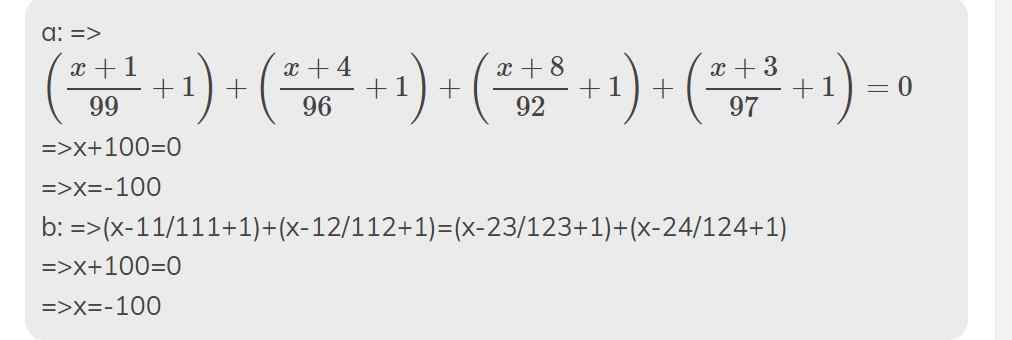

Gọi chiều rộng là x
=>Chiều dài là x+5
Theo đề, ta có: (x+5-3)(x+2)=16
=>(x+2)^2=16
=>x+2=4
=>x=2
=>Chiều dài là 7m
Chu vi lúc đầu là (2+7)*2=18(m)

Giải:
Ta có:
\(VT=\left(5a-3b+8c\right)\left(5a-3b-8c\right)\)
\(=\left(5a-3b\right)^2-\left(8c\right)^2\)
Mà \(a^2-b^2=4c^2\) nên:
\(VT=25^2-30ab+9b^2-16\left(a^2-b^2\right)\)
\(=9a^2-30ab+25b^2\)
\(=\left(3a-5b\right)^2=VP\) (Đpcm)
Ta có:
A = (5a – 3b + 8c)(5a – 3b –8c)
= (5a –3b)² – (8c)²
= (25a² – 30ab +9b²) – 64c²
Mà theo đề thì 4c² = a² –b²
Nên ta suy ra:
A = (25a² – 30ab +9b²) – 16(a² –b²)
= 9a² –30ab +25b²
= (3a –5b)²

Áp dụng bất đẳng thức cosi cho 2 số dương:
\(x+\dfrac{4}{x}\ge2\sqrt{x\cdot\dfrac{4}{x}}=4\)
Dấu '=" xảy ra khi và chỉ khi x2=4<=>x=2
\(2y+\dfrac{18}{y}\ge2\sqrt{2y\cdot\dfrac{18}{y}}=12\)
Dấu "=" xảy ra khi và chỉ khi 2y2=18<=>y=3
x+y\(\ge5\) theo đề bài
Dấu "=" xảy ra khi và chỉ khi x+y=5
=>\(\left(x+\dfrac{4}{x}\right)+\left(2y+\dfrac{18}{y}\right)+\left(x+y\right)\ge4+12+5=21\)
Dấu bằng xảy ra khi và chỉ khi x=2 y=3
rất chặt chẽ, rất logic, a nhầm 1 chỗ 2y2 = 12 chứ k phải =18, nhưng cái nhầm k có gtrị nhiu so voi cách giải ưu việt

Không dõ là hệ hay nghiêm nguyên:
PA hệ
\(\left\{\begin{matrix}2x+y=x^2\left(1\right)\\2y+x=y^2\left(2\right)\end{matrix}\right.\)
Trừ cho nhau:
\(x^2-y^2=\left(2x+y\right)-\left(2y+x\right)=2\left(x-y\right)\)
\(\left(x-y\right)\left(x+y-2\right)=0\)\(\left[\begin{matrix}x=y\\x+y-2=0\end{matrix}\right.\) thế vào cái đầu => ra nghiệm

\(\left(a+b\right)^3+\left(b+c\right)^3+\left(a+c\right)^3-3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
\(=2a^3-6abc+2b^3+2c^3\)

\(x^2+y^2+1\ge xy+x+y\)
\(\Leftrightarrow2\left(x^2+y^2+1\right)\ge2\left(xy+x+y\right)\)
\(\Leftrightarrow x^2-2xy+y^2+y^2-2y+1+x^2-2x+1\ge0\)\(\Leftrightarrow\left(x-y\right)^2-\left(y-1\right)^2-\left(x-1\right)^2\ge0\)
Đúng với mọi x , y
Đẳng thức xảy ra khi \(\left[{}\begin{matrix}\left(x-y\right)^2=0\\\left(y-1\right)^2=0\\\left(x-1\right)^2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x-y=0\\y-1=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=y\\y=1\\x=1\end{matrix}\right.\Rightarrow x=y=1\)
b, \(A=\dfrac{x-2}{x^3-x^2-x-2}=\dfrac{x-2}{x^3-2x^2+x^2-2x+x-2}\)
\(=\dfrac{x-2}{x^2\left(x-2\right)+x\left(x-2\right)+\left(x-2\right)}\)
\(=\dfrac{x-2}{\left(x^2+x+1\right)\left(x-2\right)}=\dfrac{1}{x^2+x+1}\)
\(=\dfrac{1}{x^2+2x.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}}=\dfrac{1}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\)
Ta có: \(\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(=\dfrac{1}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}\le\dfrac{4}{3}\)
Dấu " = " xảy ra khi \(\left(x+\dfrac{1}{2}\right)^2=0\Leftrightarrow x=\dfrac{-1}{2}\)
Vậy \(MAX_A=\dfrac{4}{3}\) khi \(x=\dfrac{-1}{2}\)