Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEHF có \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: EF=AH
b: Ta có: AEHF là hình chữ nhật
nên Hai đườg chéo AH và FE cắt nhau tại trung điểm của mỗi đường
hay OA=OH;OE=OF

a ) a.Vì P∈Trung trực của BC
\(\Rightarrow PB=PC\)
Ta có : AP là phân giác \(\widehat{BAC},PH\perp AB,PK\perp AC\Rightarrow PH=PK\)
Mà \(\widehat{PHB}=\widehat{PKC}=90^0\)
\(\Rightarrow\Delta PBH=\Delta PCK\) (cạnh huyền-cạnh góc vuông)
\(\Rightarrow BH=CK\)
b ) Ta có : \(PH=PK,\widehat{PHA}=\widehat{PKA}=90^0\)
\(\Rightarrow\Delta PHA=\Delta PKA\)(cạnh huyền-cạnh góc vuông)
\(\Rightarrow AH=AK\)
\(\Rightarrow\Delta AHK\) cân tại A
Mà AP là phân giác ^A
\(\Rightarrow AP\perp HK\)
Qua B kẻ BE // AK , \(E\in HK\)
\(\Rightarrow\widehat{BEH}=\widehat{AKH}\)
Do \(\Delta AHK\) cân tại A \(\Rightarrow\widehat{AKH}=\widehat{AHK}\)
\(\Rightarrow\widehat{BEH}=\widehat{BHE}\Rightarrow BH=BE\)
Mà \(BH=CK\Rightarrow BE=CK\)
Lại có BE // CK => \(\widehat{EBM}=\widehat{MCK}\)
Do M là trung điểm BC \(\Rightarrow MB=MC\Rightarrow\Delta EBM=\Delta KCM\left(c.g.c\right)\)
\(\Rightarrow\widehat{BME}=\widehat{KMC}\)
\(\Rightarrow\widehat{EMK}=\widehat{BME}+\widehat{BMK}=\widehat{CMK}+\widehat{BMK}=\widehat{BMC}=180^0\)
\(\Rightarrow E,M,K\) thẳng hàng
\(\Rightarrow H,M,K\) thẳng hàng vì E , H , K thẳng hàng
c ) Do \(PA\perp HK\) ( câu a )
\(\Rightarrow AP\perp HK=O\)
Kết hợp AH = AK \(\Rightarrow O\) là trung điểm HK
\(\Rightarrow OH=OK\)
\(\Rightarrow OA^2+OP^2+OH^2+OK^2=OA^2+OP^2+OH^2+OH^2\)
\(=\left(OA^2+OH^2\right)+\left(OP^2+OH^2\right)\)
\(=AH^2+PH^2\)
\(=AP^2,\left(PH\perp AB\right)\)

a, Xét tam giác AHB và tam giác AHC có
AB = AC ( giả thiết )
H1 = H2 ( = 90)
Ah chung
tam giác AHB = tam giác AHC ( c.g.c)
b, từ a, suy ra
- BH=HC (2 cạnh tương ứng)
- góc BAH=góc CAH (2 góc tương ứng)
c,Xét tam giác HKB và tam giác HIC có
HB = HC (từ câu b)
góc B = góc C (2 góc tương ứng)
Suy ra tam giác HKB = tam giác HIC (ch.gn)
Mik chỉ lm đc đến đây thôi còn câu d, mik ko bt lm

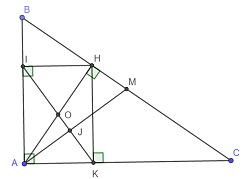
a) Xét tứ giác AIHK có \(\widehat{AIH}+\widehat{IAK}+\widehat{AKH}=270^o\Rightarrow\widehat{IHK}=90^o\)
Vậy nên \(HI\perp HK\)
b) Do IA và HK cùng vuông góc với AC nên IA // HK
Vậy thì \(\widehat{IAH}=\widehat{KHA}\) (So le trong)
Xét tam giác IAH và tam giác KHA có:
\(\widehat{AIH}=\widehat{HKA}=90^o\)
Cạnh AH chung
\(\widehat{IAH}=\widehat{KHA}\)
\(\Rightarrow\Delta AIH=\Delta HKA\) (Cạnh huyền - góc nhọn)
\(\Rightarrow IA=HK.\)
c) Xét tam giác IAH và tam giác HKI có:
\(\widehat{AIH}=\widehat{KHI}=90^o\)
Cạnh IH chung
\(IA=HK\)
\(\Rightarrow\Delta AIH=\Delta KHI\) (Hai cạnh góc vuông)
\(\Rightarrow AH=IK.\)
d) Ta thấy ngay các cặp góc so le trong bằng nhau nên \(\Delta IOA=\Delta KOH\left(g-c-g\right)\Rightarrow OI=OK,OA=OH\)
Xét tam giác vuông IAH có IO là trung tuyến ứng với cạnh huyền nên OH = OA = OI.
Vậy nên OA = OI = OH = OK.
e)
1. Nếu tam giác ABC cân thì AH là đường cao đồng thời trung tuyến. Vậy thì AH = BH = CH.
Xét tam giác cân BHA có HI là đường cao nên đồng thời là đường trung tuyến. Vậy nên I là trung điểm AB.
Hoàn toàn tương tự ta có K là trung điểm AC.
2. Tam giác ABC vuông cân tại A nên \(\widehat{ACB}=45^o\)
IA = AB/2; AK = AC/2 mà AB = AC nên AI = AK.
Vậy thì tam giác IAK cũng vuông cân tại A.
Vậy nên \(\widehat{AKI}=45^o\)
Từ đó ta có \(\widehat{AKI}=\widehat{ACB}=45^o\)
Chúng lại ở vị trí đồng vị nên suy ra IK // BC.
f) Ta có AM = MC nên \(\widehat{MAC}=\widehat{MCA}\)
Lại có \(\widehat{MCA}=\widehat{AHK}\) (Cùng phụ với góc \(\widehat{KHC}\) )
Suy ra \(\widehat{MAC}=\widehat{AHK}\)
Lại có \(\widehat{OKA}=\widehat{OHA}\)
Vậy nên \(\widehat{MAK}+\widehat{OKA}=\widehat{AHK}+\widehat{IHA}=90^o\)
Gọi J là giao điểm của AM và IK thì \(\widehat{AJK}=90^o\) hay \(KI\perp AM\)