Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì M(1;-1) là trung điểm BC và \(G\left(\frac{2}{3};0\right)\) là trọng tâm của tam giác ABC nên \(\overrightarrow{MA}=3\overrightarrow{MG}\) từ đó tìm được A(0;2)
Vì tam giác ABC cân tại A nên \(BC\perp MA\) tức là đường thẳng BC đi qua M(1;-1), nhận \(\overrightarrow{MA}=\left(-1;3\right)\) làm vec tơ pháp tuyến.
Do đó đường thẳng BC có phương trình \(-1\left(x-1\right)+3\left(y+1\right)=0\)
hay \(-x+3y+4=0\)
Do tam giác ABC vuông tại A nên MB=MC=MA=\(\sqrt{10}\)
Suy ra B, C nằm trên đường tròn \(\left(x-1\right)^2+\left(y+1\right)^2=10\)
Từ đó tọa độ B, C là nghiệm của hệ phương trình
\(\begin{cases}-x+3y+4=0\\\left(x-1\right)^2+\left(y+1\right)^2=10\end{cases}\)
Giải hệ phương trình thu được (x;y) = (4;0) và (x;y) = (-2;2)
Vậy A(0;2), B(4; 0), C(-2;-2)

AM vuông góc với DE chứ.
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right);\overrightarrow{DE}=\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{DE}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}.\overrightarrow{AE}-\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AC}.\overrightarrow{AE}\right)\)
\(=\dfrac{1}{2}\left[AB.AE.cos\left(\widehat{BAC}+90^o\right)-AC.AD.cos\left(\widehat{BAC}+90^o\right)-AB.AD.cos90^o+AC.AE.cos90^o\right]\)
\(=0\)
\(\Rightarrow AM\perp DE\)

a) Nếu ABC là một tam giác cân thì ABC là tam giác đều
Đây là mệnh đề sai
b) Nếu ABC là một tam giác cân và có một góc bằng 60o thì ABC là một tam giác đều
Đây là mệnh đề đúng

bài 1:
\(16\frac{2}{7}:\left(-\frac{2}{5}\right)-28\frac{2}{7}:\left(-\frac{2}{5}\right)\\ =\left(16\frac{2}{7}-28\frac{2}{7}\right):\left(-\frac{2}{5}\right)\\ =\left(-12\right):\left(-\frac{2}{5}\right)\\ =12:\frac{2}{5}\\ =\frac{6.5}{1}\\ =30\)
Bài 2:
Gọi độ dài 3 cạnh của tam giác là x; y; z; ta có:
Chu vi của tam giác là 36
=> x + y + z = 36
Ba cạnh của tam giác tỉ lệ với 3; 4; 5
=> \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{36}{12}=3\)
x/3 = 3 => x = 3.3 = 9 cm
y/4 = 3 => y = 3.4 = 12 cm
z/5 = 3 => z = 3.5 = 15 cm
Vậy độ dài 3 cạnh của tam giác lần lượt là 9; 12; 12 (cm)
Bài 1:
\(16\frac{2}{7}:\left(-\frac{2}{5}\right)-23\frac{2}{7}:\left(-\frac{2}{5}\right)=-7:\left(-\frac{2}{5}\right)=\frac{35}{2}\)
Bài 2:
Gọi độ dài các cạnh của tam giác là a,b,c
theo đề bài ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a+b+c=36
Apd đụng tc của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{36}{12}=3\)
=>\(\begin{cases}a=9\\b=12\\c=15\end{cases}\)
Vậy độ dài các cạnh của tam giác là 9;12;15

Gọi ( O;R ) , ( I ;r ) lần lượt là các đường tròn ngoại tiếp tam giác ABC, DEF
Tam giác ABC ~ Tam giác DEF ( vì \(\widehat{ABC}=\widehat{DEF};\widehat{BAC}=\widehat{EDF}\)) \(\Rightarrow\widehat{ABC}=\widehat{DEF}\)
\(\widehat{ACB},\widehat{DEF}\)nhọn nên \(\widehat{ACB}=\frac{1}{2}\widehat{AOB};\widehat{DEF}=\frac{1}{2}\widehat{DIE}\)( hệ quả góc nội tiếp )
\(\Rightarrow\widehat{AOB}=\widehat{DIE}\)
\(OA=OB\left(=R\right)\Rightarrow\Delta OAB\)cân tại O
\(ID=IE\left(=r\right)\Rightarrow\Delta IDE\)cân tại I
Do đó Tam giác OAB ~ Tam giác IDE \(\Rightarrow\frac{OA}{ID}=\frac{AB}{DE}\Rightarrow\frac{R}{r}=\frac{3DE}{DE}\)
\(\Rightarrow R=3r\) ( đpcm)
Gọi ( O; R ), ( I; R ) lần lượt là các đường tròn ngoại tiếp tam giác ABC, DEF
Tam giác ABC ~ Tam giác DEF ( vì \(\widehat{ABC}=\widehat{DEF;}\widehat{BAC}=\widehat{EDF}\) ) \(\Rightarrow\widehat{ABC}=\widehat{DEF}\)
\(\widehat{ABC}=\widehat{DEF}\)nhọn nên \(\widehat{ACB}=\frac{1}{2}\widehat{AOB};\widehat{DEF}=\frac{1}{2}\widehat{DIE}\)(hệ quả góc nội tiếp )
\(\Rightarrow\widehat{AOB}=\widehat{DIE}\)
\(OA=OA\left(=R\right)\Rightarrow\Delta OAB\)cân tại O
Do đó Tam giác OAB ~ Tam giác IDE\(\Rightarrow\frac{OA}{ID}=\frac{AB}{DE}\Rightarrow\frac{R}{r}=\frac{3DE}{DE}\)
\(\Rightarrow R=3r\left(đpcm\right)\)
Rất vui vì giúp đc bạn <3

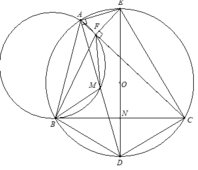
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).
Gọi số đo của 3 góc trong tam giác đó lần lượt là \(\widehat{A}=a,\widehat{B}=b,\widehat{C}=c\)
Theo bài ta có :
\(a+b+c=180^0\) (định lí tổng 3 góc trong tam giác)
\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}\)
Theo t,c dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{1}=\dfrac{b}{2}=\dfrac{c}{3}=\dfrac{a+b+c}{1+2+3}=\dfrac{180^0}{6}=30^0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{1}=30^0\\\dfrac{b}{2}=30^0\\\dfrac{c}{3}=30^0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=30^0\\b=60^0\\c=90^0\end{matrix}\right.\) \(\Leftrightarrow\Delta ABC\) vuông
thank you bạn nhé