Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
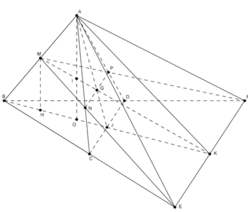
Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
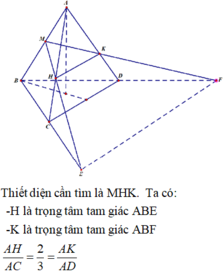
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó
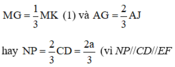
và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là
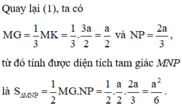
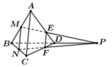
Do E, F lần lượt là trọng tâm các tam giác ABP, BCP nên
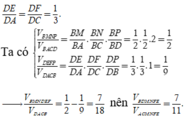
Chọn B.
Phương pháp:
Sử dụng tỉ số diện tích, tỉ số thể tích để tính thể tích khối tứ diện MBSI thông qua thể tích khối tứ diện vuông SABC.
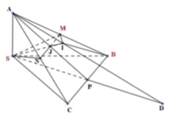
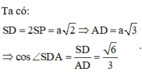
Áp dụng định lí Menelaus trong tam giác APD ta có:
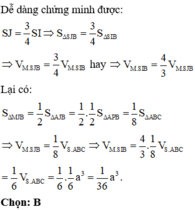
Đáp án A
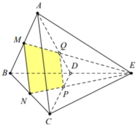
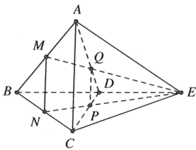
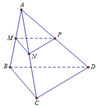
Nối 
chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
Dễ thấy P,Q lần lượt là trọng tâm của ∆BCE, ∆ABE
Gọi S là diện tích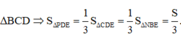 
Họi h là chiều cao của tứ diện ABCD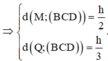 
Khi đó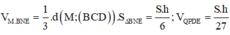 
Suy ra
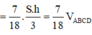
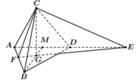
Gọi G là trọng tâm tam giác ABD suy ra C G ⊥ A B D
Do đó mặt phẳng cần dựng là (CEG). Gọi F = E G ∩ A B
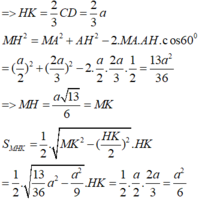
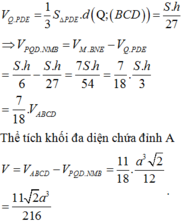
Phương pháp:
Sử dụng lý thuyết khối đa diện để làm bài toán.
Cách giải:
Khối đa diện được tạo từ 6 đỉnh là 6 trung điểm của các cạnh của tứ diện đều là khối bát diện đều có 6 đỉnh, 12 cạnh và 8 mặt.
Khối bát diện đều là khối đa diện có 9 mặt đối xứng.
Chọn: D