PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
3
0
4 tháng 4 2018
a) Ta có: P(x) = 0 khi 3 – 2x = 0
=>-2x = -3 => x = \(\frac{3}{2}\)
b) Q(x) =x2 +2 là đa thức không có nghiệm vì
x2 ≥ 0
2 > 0 (theo quy tắc nhân hai số hữu tỉ cùng dấu)
=>x2 + 2 > 0 với mọi x
Nên Q(x) không có nghiệm trong R
SG
4 tháng 4 2018
a) Ta có:
P(x) = 0 khi 3 - 2x = 0
=> -2x = -3 => x = \(\frac{3}{2}\)
b) Q(x) = x2+ 2 là đa thức ko có nghiệm vì:
x2\(\ge\)0
2 > 0 ( theo quy tắc nhân hai số hữu tỉ cùng dấu.)
=> x2 + 2 > 0 với mọi x
Nên Q(x) ko có nghiệm trong R.
TT
2
8 tháng 4 2021
a) f(x) = 0 ⇔ 4 - 5x = 0 ⇔ x = \(\dfrac{4}{5}\)
Nghiệm của f(x) là \(\dfrac{4}{5}\)
b)Không có nghiệm vì Với mọi x ∈ R thì \(x^2\) ≥ 0 ⇔ \(x^2\) + 4 ≥ 4 > 0
Do đó \(x^2\) + 4 > 0 hay \(x^2\) + 4 ≠ 0
Vậy f(x) không có nghiệm
H
19 tháng 4 2017
a) Ta có: P(x) = 0 khi 3 – 2x = 0
=>-2x = -3 => x = \(\dfrac{3}{2}\)
b) Q(x) =x2 +2 là đa thức không có nghiệm vì
x2 ≥ 0
2 > 0 (theo quy tắc nhân hai số hữu tỉ cùng dấu)
=>x2 + 2 > 0 với mọi x
Nên Q(x) không có nghiệm trong R
TP
19 tháng 4 2017
a) Ta có P(x) = 0 khi 3 – 2x = 0
b) Đa thức Q(x) không có nghiệm, bởi vì:
x2 ≥ 0 với mọi x thuộc R.
2 > 0
\(\Rightarrow\) Q(x) = x2 + 2 > 0 với mọi x thuộc R.
Do đó, không có giá trị x nào thuộc R để Q(x) = 0 hay đa thức Q(x) không có nghiệm.
ND
3
17 tháng 4 2016
Giả sử đa thức Q(x) tồn tại một nghiệm n nào đó(n\(\in\) R)
Khi đó: Q(x)= x.2+2 =0
2x = -2 => x = -1
Vậy với giá trị x = -1 thì đa thức Q(x)= 0 => Điều giả sử là đúng. Vậy đa thức Q(x) có nghiệm)
PT
1
CM
5 tháng 6 2019
Giá trị của đa thức x3 – 4x tại x = -2 là: (-2)3 – 4.( - 2) = – 8 + 8 = 0
Giá trị của đa thức x3 – 4x tại x = 0 là: 03 – 4.0 = 0 – 0 = 0
Giá trị của đa thức x3 – 4x tại x = 2 là: 23 – 4.2 = 8 – 8 = 0
Vậy x = -2; x = 0 và x = 2 có phải là các nghiệm của đa thức x3 – 4x
( vì tại các giá trị đó của biến, đa thức có giá trị bằng 0)
6 tháng 4 2022
\(\Leftrightarrow x^3-4x=0\\ \Leftrightarrow x\left(x^2-4\right)=0\\ \Leftrightarrow x\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
Vậy tập nghiệm của pt \(S=\left\{0;2;-2\right\}\)
MH
12 tháng 5 2022
a) \(P\left(x\right)=0\Rightarrow x^{2016}-x^{2014}=0\Rightarrow x^{2014}\left(x^2-1\right)=0\)
TH1: \(x^{2014}=0\Rightarrow x=0\)
TH2: \(x^2-1=0\Rightarrow x=\pm1\)
Vậy \(P\left(x\right)\) có nghiệm là \(x=0,x=1,x=-1\)
b) Xét \(x< 0\)
Ta có: \(x^{2016}>0\Rightarrow-x^{2016}< 0\); \(2015x< 0\)
\(\Rightarrow Q\left(x\right)=-x^{2016}+2015x-1< 0\)
Vậy \(Q\left(x\right)\) không có nghiệm âm
12 tháng 5 2022
a, Đặt \(P\left(x\right)=x^{2016}-x^{2014}=0\Leftrightarrow x^{2014}\left(x^2-1\right)=0\Leftrightarrow x=0;x=-1;x=1\)
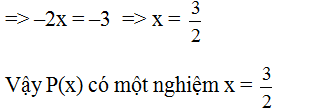
Q(x) = x2 + 2 là đa thức không có nghiệm vì
x2 ≥ 0 với mọi x
(vì lũy thừa với số mũ chẵn của 1 số bất kỳ là 1 số không âm)
⇒ Q(x) = x2 + 2 > 0 với mọi x
Hay Q(x) = x2 + 2 ≠ 0 với mọi x.