Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(m_{cr}=m_{Fe}=12.8\left(g\right)\)
\(NaOH+Al+H_2O\rightarrow NaAlO_2+\dfrac{3}{2}H_2\)
\(m_{Al}=m_{hh}-m_{Fe}=18.2-12.8=5.4\left(g\right)\)
\(\%m_{Al}=\dfrac{5.4}{18.2}\cdot100\%=29.67\%\)

$NaOH + HCl \to NaCl + H_2O$
$n_{HCl\ dư} = n_{NaOH} = 0,05.2 = 0,1(mol)$
Gọi $n_{Fe} = a ; n_{Zn} = b \Rightarrow 56a + 65b = 12,1(1)$
$Fe + 2HCl \to FeCl_2 + H_2$
$Zn + 2HCl \to ZnCl_2 + H_2$
$n_{HCl} = 2a + 2b = 0,5 -0,1 = 0,4(2)$
Từ (1)(2) suy ra a = b = 0,1
$\%m_{Fe} = \dfrac{0,1.56}{12,1}.100\% = 46,28\%$
$\%m_{Zn} = 100\% -46,28\% = 53,72\%$
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
\(Zn+2HCl\rightarrow ZnCl_2+H_2\)
\(HCl_{dư}+NaOH\rightarrow NaCl+H_2O\)
Gọi x, y lần lượt là số mol Fe, Zn, theo đề ta có:
\(\left\{{}\begin{matrix}56x+65y=12,1\\2x+2y=0,5.1-0,05.2\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=0,1\\y=0,1\end{matrix}\right.\)
=> \(\%m_{Fe}=\dfrac{0,1.56}{12,1}=46,28\%\)
=> \(\%m_{Zn}=100-46,28=53,72\%\)

\(a)2Al+HCl\rightarrow2AlCl_3+3H_2\\ Fe+2HCl\rightarrow FeCl_2+H_2\)
b) \(n_{HCl}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\\ Gọi:n_{Al}=x\left(mol\right);n_{Fe}=y\left(mol\right)\\ Tacó:\left\{{}\begin{matrix}27x+56y=m_{hh}\\\dfrac{3}{2}x+y=0,4\end{matrix}\right.\)
Đề thiếu dữ kiện, xem lại đề nha bạn !

a, \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
b, Ta có: 27nAl + 56nFe = 5,5 (1)
Theo PT: \(n_{H_2}=\dfrac{3}{2}n_{Al}+n_{Fe}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{Al}=0,1\left(mol\right)\\n_{Fe}=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,1.27}{5,5}.100\%\approx49,09\%\\\%m_{Fe}\approx50,91\%\end{matrix}\right.\)

a, Ta có: 27nAl + 56nFe = 22 (1)
PT: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
Theo PT: \(n_{H_2}=\dfrac{3}{2}n_{Al}+n_{Fe}=\dfrac{19,832}{24,79}=0,8\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}m_{Al}=0,4\left(mol\right)\\n_{Fe}=0,2\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,4.27}{22}.100\%\approx49,09\%\\\%m_{Fe}\approx50,91\%\end{matrix}\right.\)
b, \(n_{HCl}=2n_{H_2}=1,6\left(mol\right)\)
\(\Rightarrow C_{M_{HCl}}=\dfrac{1,6}{0,5}=3,2\left(M\right)\)

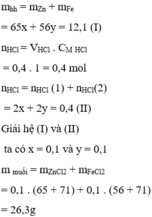

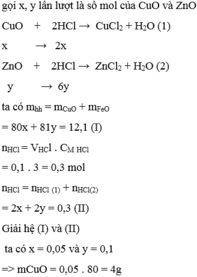
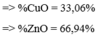

2Al + 6HCl ---> 2AlCl3 + 3H2
x -------------> 3/2 x (mol)
Fe + 2HCl ----> FeCl2 + H2
y --------------> y (mol)
=> \(\left\{{}\begin{matrix}27x+56y=5,5\\3x+2y=0,4\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=0,1\\y=0,05\end{matrix}\right.\)
=> %mAl = 0,1.27.100%/5,5= 49,09%
%mFe = 100% - 49,09% = 50,91%