
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

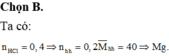

Gọi số mol của Mg, Al ,Cu có trong hỗn hợp lần lượt là a, b, c (mol) (a,b,c>0)
2Mg + O2 --t*--> 2MgO (1)
...a............................a (mol)
4Al + 3O2 --t*--> 2Al2O3 (2)
...b............................b/2 (mol)
2Cu + O2 --t*--> 2CuO (3)
...c.............................c (mol)
Khi m (g) hỗn hợp 3 kim loại trên tác dụng với HCl dư => Cu không phản ứng với HCl
Mg + 2HCl ---> MgCl2 + H2 (4)
..a...................................a (mol)
2Al + 6HCl ---> 2AlCl3 + 3H2 (5)
..b....................................3b/2 (mol)
Theo đầu ta có 24a + 27b + 64c = m (I)
..........................40a + 51b + 80c = 1,72m (II)
.......................... a + 3b/2 + 0c = 0,952m/22,4 (III)
Vì m(g) là 1 đại lượng chưa biết và cả 3 pt trên đều chứa m ở vế phải nên ta có thể giả sử m=1 (g) (Khi thay
m=1 không ảnh hưởng đến % khối lượng các chất có tronh hỗn hợp)
Khi đó thay m=1 vào (I), (II) (III) ta được:
(I) <=> 24a + 27b + 64c = 1
(II) <=> 40a + 51b + 80c = 1,72
(III) <=> a + 3b/2 +0c=0,0425
Giải hệ phương trình 3 ẩn (cái này nên dùng bằng máy tính là nhanh nhất) trên ta được
a = 0,0125 (mol) => mMg = 0,3g => %Mg=0,3/1.100%=30%
b = 0,02 (mol) => mAl = 0,54g => %Al= 0,54/1.100%=54%
c = 0,0025 (mol) => mCu = 0,16g => %Cu=0,16/1.100%=16%

Ta có:
Hàm \(\Psi\)được gọi là hàm chuẩn hóa nếu: \(\int\Psi.\Psi^{\circledast}d\tau=1hay\int\Psi^2d\tau=1\)
Hàm \(\Psi\)chưa chuẩn hóa là: \(\int\left|\Psi\right|^2d\tau=N\left(N\ne1\right)\)
Để có hàm chuẩn hóa, chia cả 2 vế cho N,ta có:
\(\frac{1}{N}.\int\left|\Psi\right|^2d\tau=1\Rightarrow\frac{1}{N}.\int\Psi.\Psi^{\circledast}d\tau=1\)
Trong đó: \(\Psi=\frac{1}{\sqrt{N}}.\Psi\)là hàm chuẩn hóa; \(\frac{1}{\sqrt{N}}\)là thừa số chuẩn hóa
Ta có:
\(\frac{1}{N}.\int\Psi.\Psi^{\circledast}d\tau=\frac{1}{N}.\int\left|\Psi\right|^2d\tau=1\Leftrightarrow\frac{1}{N}.\iiint\left|\Psi\right|^2dxdydz=1\)
Chuyển sang tọa độ cầu, ta có: \(\begin{cases}x=r.\cos\varphi.sin\theta\\y=r.sin\varphi.sin\theta\\z=r.\cos\theta\end{cases}\)với \(\begin{cases}0\le r\le\infty\\0\le\varphi\le2\pi\\0\le\theta\le\pi\end{cases}\)
\(\Rightarrow\frac{1}{N}.\iiint\left(r.\cos\varphi.sin\theta\right)^2.e^{-\frac{r}{a_o}}.r^2.sin\theta drd\varphi d\theta=1\)
\(\Leftrightarrow\frac{1}{N}.\int\limits^{\infty}_0r^4.e^{-\frac{r}{a_o}}dr.\int\limits^{2\pi}_0\cos^2\varphi d\varphi.\int\limits^{\pi}_0sin^3\theta d\theta=1\)
\(\Leftrightarrow\frac{1}{N}.\frac{4!}{\left(\frac{1}{a_o}\right)^5}.\int\limits^{2\pi}_0\frac{\cos\left(2\varphi\right)+1}{2}d\varphi\int\limits^{\pi}_0\frac{3.sin\theta-sin3\theta}{4}d\theta=1\)(do \(\int\limits^{\infty}_0x^n.e^{-a.x}dx=\frac{n!}{a^{n+1}}\))
\(\Leftrightarrow\frac{1}{N}.24.a^5_o.\frac{4}{3}.\pi=1\)
\(\Leftrightarrow\frac{1}{N}=\frac{1}{32.a^5_o.\pi}\)
\(\Rightarrow\)Thừa số chuẩn hóa là: \(\frac{1}{\sqrt{N}}=\sqrt{\frac{1}{32.a^5_o.\pi}}\); Hàm chuẩn hóa: \(\Psi=\frac{1}{\sqrt{N}}.\Psi=\sqrt{\frac{1}{32.a^5_o.\pi}}.x.e^{-\frac{r}{2a_o}}\)
áp dụng dk chuẩn hóa hàm sóng. \(\int\psi\psi^{\cdot}d\tau=1.\)
ta có: \(\int N.x.e^{-\frac{r}{2a_0}}.N.x.e^{-\frac{r}{2a_0}}.d\tau=1=N^2.\int_0^{\infty}r^4e^{-\frac{r}{a_0}}dr.\int_0^{\pi}\sin^3\theta d\tau.\int^{2\pi}_0\cos^2\varphi d\varphi=N^2.I_1.I_2.I_3\)
Thấy tích phân I1 có dạng tích phân hàm gamma. \(\int^{+\infty}_0x^ne^{-ax}dx=\int^{+\infty}_0\frac{\left(\left(ax\right)^{n+1-1}e^{-ax}\right)d\left(ax\right)}{a^{n+1}}=\frac{\Gamma\left(n+1\right)!}{a^{n+1}}=\frac{n!}{a^{n+1}}.\)
.áp dụng cho I1 ta được I\(I1=4!.a_0^5=24a^5_0\). tính \(I2=\int_0^{\pi}\sin^3\theta d\theta=\int_0^{\pi}\left(\cos^2-1\right)d\left(\cos\theta\right)=\frac{4}{3}\). tính tp \(I3=\int_0^{2\pi}\cos^2\varphi d\varphi=\int_0^{2\pi}\frac{\left(1-\cos\left(2\varphi\right)\right)}{2}d\varphi=\pi\)
suy ra \(\frac{N^2.24a_0^5.\pi.4}{3}=1\). vậy N=\(N=\frac{1}{\sqrt{32\pi a_0^5}}\). hàm \(\psi\) sau khi chiuẩn hóa có dạng \(\psi=\frac{1}{\sqrt{\pi32.a_0^5}}x.e^{-\frac{r}{2a_0}}\)

ct A va AO

A(Fe, S) ==nung==> B(Fe, S, FeS) ==HCl==> C(H2, H2S)
B(Fe, S, FeS) ==nung==> (Fe2O3, SO2)
Bằng phương pháp sơ đồ đường chéo bạn dễ dàng tính được tỉ lệ nH2/nH2S = 1/3
Mà nH2 + nH2S = V
=> nH2 = 0,25V và nH2S = 0,75V
Sau khi viết tất cả các phương trình phản ứng, bạn dễ dàng tính được những kết quả sau :
nFe (trong B) = nH2 = 0,25V mol => mFe = 14V g
nFeS (trong B) = nH2S = 0,75V mol => mFeS = 66V g
Phản ứng của B với O2 :
4FeS + 7O2 = 2Fe2O3 + 4SO2
0,75V....1,3125V mol
S + O2 = SO2
x.....x
Ta có 1,3125V + x = V'' => nS = x = V'' - 1,3125V
=> mS = 32V'' - 42V
mB = mFe + mS + mFeS = 14V + 32V'' - 42V + 66V = 38V + 32V'' g
b. nS = V'' - 1,3125V => V'' > 1,3125V => V''/V > 1,3125

a, Ta có:
Hai hàm sóng trực giao nhau khi \(I=\int\psi_{1s}.\psi_{2s}d\psi=0\) \(\Leftrightarrow I=\iiint\psi_{1s}.\psi_{2s}dxdydz=0\)
Chuyển sang tọa độ cầu ta có: \(\begin{cases}x=r.\cos\varphi.sin\theta\\y=r.\sin\varphi.sin\theta\\z=r.\cos\theta\end{cases}\)
\(\Rightarrow\)\(I=\frac{a^3_o}{4.\sqrt{2.\pi}}\int\limits^{\infty}_0\left(2-\frac{r}{a_o}\right).e^{-\frac{3.r}{2.a_o}}.r^2.\sin\theta dr\int\limits^{2\pi}_0d\varphi\int\limits^{\pi}_0d\theta\)
\(=a^3_o.\sqrt{\frac{\pi}{2}}\)(.\(2.\int\limits^{\infty}_0r^2.e^{-\frac{3.r}{2.a_o}}dr-\frac{1}{a_o}.\int\limits^{\infty}_0r^3.e^{-\frac{3.r}{2.a_o}}dr\))
\(=a_o.\sqrt{\frac{\pi}{2}}.\left(2.I_1-\frac{1}{a_o}.I_2\right)\)
Tính \(I_1\):
Đặt \(r^2=u\); \(e^{-\frac{3r}{2a_o}}dr=dV\)
\(\Rightarrow\begin{cases}2.r.dr=du\\-\frac{2a_o}{3}.e^{-\frac{3r}{2a_o}}=V\end{cases}\) \(\Rightarrow I_1=-r^2.\frac{2a_o}{3}.e^{-\frac{3r}{2a_o}}+\frac{4.a_o}{3}.\int\limits^{\infty}_0r.e^{-\frac{3r}{2a_o}}dr\)\(=0+\frac{4a_o}{3}.I_{11}\)
Tính \(I_{11}\):
Đặt r=u; \(e^{-\frac{3r}{2a_o}}dr=dV\)\(\Rightarrow\begin{cases}dr=du\\-\frac{2a_o}{3}.e^{-\frac{3r}{2a_o}}=V\end{cases}\)\(\Rightarrow I_{11}=0+\frac{2a_0}{3}.\int\limits^{\infty}_0e^{-\frac{3r}{2a_o}}dr=\frac{4a^2_o}{9}\)
\(\Rightarrow2.I_1=2.\frac{4a_o}{3}.\frac{4a_o^2}{9}=\frac{32a^3_o}{27}\)
Tính \(I_2\):
Đặt \(r^2=u;e^{-\frac{3r}{2a_o}}dr=dV\) \(\Rightarrow\)\(3r^2dr=du;-\frac{2a_o}{3}.e^{-\frac{3r}{2a_o}}=V\)
\(\Rightarrow I_2=0+2.a_o.\int\limits^{\infty}_0r^2.e^{-\frac{3r}{2a_o}}dr\)\(\Rightarrow\frac{1}{a_o}.I_2=2a_o.\frac{16a^3_o}{27}.\frac{1}{a_o}=\frac{32a^3_o}{27}\)
\(\Rightarrow I=a^3_o.\sqrt{\frac{\pi}{2}}.\left(\frac{32a^3_o}{27}-\frac{32a^3_o}{27}\right)=0\)
Vậy hai hàm sóng này trực giao với nhau.
b,
Xét hàm \(\Psi_{1s}\):
Hàm mật độ sác xuất là: \(D\left(r\right)=\Psi^2_{1s}=\frac{1}{\pi}.a^3_o.e^{-\frac{2r}{a_o}}\)
\(\Rightarrow D'\left(r\right)=-\frac{2.a_o^2}{\pi}.e^{-\frac{2r}{a_o}}=0\)
\(\Rightarrow\)Hàm đạt cực đại khi \(r\rightarrow o\) nên hàm sóng có dạng hình cầu.
Xét hàm \(\Psi_{2s}\):
Hàm mật độ sác xuất: \(D\left(r\right)=\Psi_{2s}^2=\frac{a^3_o}{32}.\left(2-\frac{r}{a_o}\right)^2.e^{-\frac{r}{a_0}}\)\(\Rightarrow D'\left(r\right)=\left(2-\frac{r}{a_o}\right).e^{-\frac{r}{a_o}}.\left(-4+\frac{r}{a_o}\right)=0\)
\(\Rightarrow r=2a_o\Rightarrow D\left(r\right)=0\); \(r=4a_o\Rightarrow D\left(r\right)=\frac{a^3_o}{8}.e^{-4}\)
Vậy hàm đạt cực đại khi \(r=4a_o\), tại \(D\left(r\right)=\frac{a^3_o}{8}.e^{-4}\)
hai hàm trực giao: I=\(\int\)\(\Psi\)*\(\Psi\)d\(\tau\)=0
Ta có: I=\(\int\limits^{ }_x\)\(\int\limits^{ }_y\)\(\int\limits^{ }_z\)\(\Psi\)*\(\Psi\)dxdydz=0
=\(\int\limits^{ }_r\)\(\int\limits^{ }_{\theta}\)\(\int\limits^{ }_{\varphi}\)\(\Psi\)1s\(\Psi\)2sr2sin\(\theta\)drd\(\theta\)d\(\varphi\)
=\(\int\limits^{\infty}_0\)\(\int\limits^{\pi}_0\)\(\int\limits^{2\pi}_0\)(2-\(\frac{r}{a_0}\)).e-3r/a0r2sin\(\theta\)drd\(\theta\)d\(\varphi\)
=C.\(\int\limits^{\infty}_0\)(2-\(\frac{r}{a_0}\)).e-3r/a0r2dr.\(\int\limits^{\pi}_0\)sin\(\theta\)\(\int\limits^{2\pi}_0\)d\(\varphi\)
với C=\(\frac{1}{4\sqrt{2\pi}}\)a0-3
Xét tích phân: J=\(\int\limits^{\infty}_0\)(2-\(\frac{r}{a_0}\)).e-3r/a0r2dr
=\(\int\limits^{\infty}_0\)(2r2- \(\frac{r^3}{a_0}\)).e-3r/a0dr
=\(\int\limits^{\infty}_0\)(2r2- \(\frac{r^3}{a_0}\)).\(\frac{-2a_0}{3}\)de-3r/a0
=\(\frac{-2a_0}{3}\).((2r2-\(\frac{r^3}{a_0}\))e-3r/a0\(-\)\(\int\)(4r-\(\frac{3r^2}{a_0}\))e-3r/adr)
=\(\frac{-2a_0}{3}\)((2r2-\(\frac{r^3}{a_0}\))e-3r/a0 - \(\int\)(4r-\(\frac{3r^2}{a_0}\)).\(\frac{-2a_0}{3}\)de-3r/a)
=\(\frac{-2a_0}{3}\)((2r2-\(\frac{r^3}{a_0}\))e-3r/a0 +\(\frac{2a_0}{3}\).((4r-\(\frac{3r^2}{a_0}\))e-3r/a0 - \(\int\)(4 - \(\frac{6r}{a_0}\))e-3r/a0dr))
=\(\frac{-2a_0}{3}\)((2r2-\(\frac{r^3}{a_0}\))e-3r/a0 +\(\frac{2a_0}{3}\).((4r-\(\frac{3r^2}{a_0}\))e-3r/a0- \(\int\)(4 - \(\frac{6r}{a_0}\))\(\frac{-2a_0}{3}\).de-3r/a0))
=\(\frac{-2a_0}{3}\)(((2r2-\(\frac{r^3}{a_0}\))e-3r/a0 +\(\frac{2a_0}{3}\).((4r-\(\frac{3r^2}{a_0}\))e-3r/a0+\(\frac{2a_0}{3}\)((4-\(\frac{6r}{a_0}\)).e-3r/a0 + \(\int\)(\(\frac{6}{a_0}\)e-3r/a0dr)))
=\(\frac{-2a_0}{3}\)(((2r2-\(\frac{r^3}{a_0}\))e-3r/a0 +\(\frac{2a_0}{3}\).((4r-\(\frac{3r^2}{a_0}\))e-3r/a0+\(\frac{2a_0}{3}\)((4-\(\frac{6r}{a_0}\)).e-3r/a0 + \(\int\)(\(\frac{6}{a_0}\).\(\frac{-2a_0}{3}\)de-3r/a0)))
=\(\frac{-2a_0}{3}\)((((2r2-\(\frac{r^3}{a_0}\))e-3r/a0 +\(\frac{2a_0}{3}\).((4r-\(\frac{3r^2}{a_0}\))e-3r/a0+\(\frac{2a_0}{3}\)((4-\(\frac{6r}{a_0}\)).e-3r/a0 - 4.e-3r/a0))))

MgCO3 + 2HCl → MgCl2 + CO2 + H2O (1)
BaCO3 + 2HCl → BaCl2 + CO2 + H2O (2)
CO2 + Ca(OH)2 → CaCO3↓ + H2O. (3)
Theo (1), (2) và (3), để lượng kết tủa B thu được là lớn nhất thì:
nCO2 = nMgCO3 + nBaCO3 = 0,2 mol
Ta có: 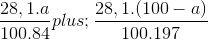 = 0,2
= 0,2
=> a = 29,89.

n SO2 = 0,25 mol