Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$M,N$ lần lượt là trung điểm $AB, AC$ nên $MN$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow MN\parallel BC$ hay $MN\parallel HP$
$\Rightarrow MNPH$ là hình thang $(*)$
Mặt khác:
Tam giác vuông $ABH$ có $HM$ là đường trung tuyến ứng với cạnh huyền nên $HM=\frac{AB}{2}=MB$ (bổ đề quen thuộc)
$\Rightarrow $MHB$ cân tại $M$
$\Rightarrow \widehat{MHB}=\widehat{MBH}$
Mà $\widehat{MBH}=\widehat{NPC}$ (hai góc đồng vị với $NP\parallel AB$)
$\Rightarrow \widehat{MHB}=\widehat{NPC}$
$\Rightarrow 180^0-\widehat{MHB}=180^0-\widehat{NPC}$
Hay $\widehat{MHP}=\widehat{NPH}(**)$
Từ $(*); (**)\Rightarrow $MNPH$ là hình thang cân (đpcm)

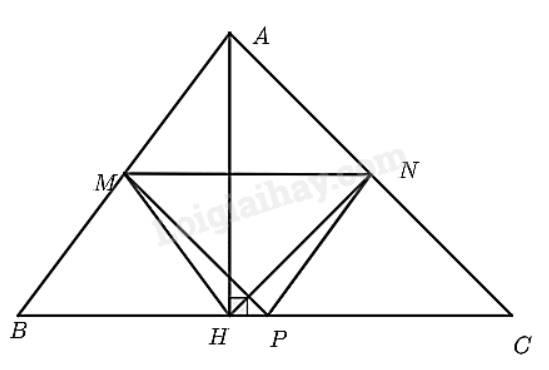
- Vì \(M\) là trung điểm của \(AB;N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\). Do đó, \(MN//BC\) (tính chất đường trung bình).
\( \Rightarrow MN//HP\left( {H;P \in BC} \right)\)
Xét tứ giác \(MNPH\) có: \(MN//HP \Rightarrow \) tứ giác \(MNPH\) là hình thang.
- Vì \(M\) là trung điểm của \(AB;P\) là trung điểm của \(AC\) nên \(MP\) là đường trung bình của tam giác \(ABC\). Do đó, \(MP = \frac{1}{2}AC\) (tính chất đường trung bình) (1).
- Xét tam giác \(AHC\) vuông tại \(H\) có:
\(N\)là trung điểm của \(AC\) nên \(HN = \frac{1}{2}AC\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (2).
Từ (1) và (2) suy ra \(MP = HN\).
Xét hình thang \(MNPH\) có: \(MP = HN\) (chứng minh trên).
Do đó, hình thang \(MNPH\) là hình thang cân (dấu hiệu nhận biết hình thang cân).
bài này dễ lắm
câu a bạn tự làm nha vì nó quá dễ rồi
b) Mình xin đính chính lại là P là trung điểm của AB chứ không phải B, bạn viết lộn rùi
Gọi O là giao điểm của PN và AH
Ta có: P là trung điểm của AB (gt)
BO// BH ( t/c đướng trung bình, đã cm ở câu a)
=> O là trung điểm của AH => AO = OH
Xét tam giác APO và tam giác HPO có:
BO là cạnh chung
Góc POH = góc POA = 90 độ ( PN là đướng trung trực của AH )
AO = HO (cmt)
=> Tam giác APO = tam giác HPO ( c-g-c)
=> Góc OPH = góc OPA ( 2 góc tương ứng) (5)
Ta có: PN là đướng trung bình của tam giác ABC ( cm ở câu a)
=> PN = \(\frac{1}{2}\)BC (1) => PN // BC
Mà M là trung điểm của BC (gt) => BM = MC = \(\frac{1}{2}\)BC (2)
Từ (1) và (2) => PN = BM = MC hay PN = BM, PN = BM (3)
Ta lại có: PN//BC => PN//BM (4)
Từ (3) và ( 4) => PNMB là hình bình bình hành => NM //PB => NM//AP => góc OPA = góc MNP ( cặp góc slt) (6)
Mà PN//HM ( PN//BC, t/c đướng trung bình) => MNPH là hình thang (7)
Từ(5), (6) và (7) MNPH là hình thang cân
BO sao lại sog song với BH