
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Thay a=-2 vào pt, ta được:
\(-2x^2-2\cdot\left(-2-1\right)x-2+1=0\)
\(\Leftrightarrow-2x^2+6x-1=0\)
\(\Leftrightarrow2x^2-6x+1=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot2\cdot1=36-8=28>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{6-2\sqrt{7}}{2}=3-\sqrt{7}\\x_2=3+\sqrt{7}\end{matrix}\right.\)
b: Để phương trình có hai nghiệm phân biệt thì
\(\left\{{}\begin{matrix}\left(-2a+2\right)^2-4a\left(a+1\right)>0\\a< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^2-8a+4-4a^2-4a>0\\a< >0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-12a>-4\\a< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a< >0\\a< \dfrac{1}{3}\end{matrix}\right.\)

Gọi tỉ lệ cắt giảm mỗi năm của công ty là \(x\left(\%\right)\) hay \(\dfrac{x}{100}\) với \(0\le x\le100\)
Số công nhân còn lại sau năm thứ nhất là:
\(10000\left(1-\dfrac{x}{100}\right)\)
Số công nhân còn lại sau năm thứ hai là:
\(10000.\left(1-\dfrac{x}{100}\right)\left(1-\dfrac{x}{100}\right)=10000.\left(1-\dfrac{x}{100}\right)^2\)
Do sau 2 năm công ty còn lại 9000 công nhân nên:
\(10000\left(1-\dfrac{x}{100}\right)^2=9000\)
\(\Rightarrow1-\dfrac{x}{100}=\dfrac{3}{\sqrt{10}}\Rightarrow x=100-30\sqrt{10}\) (%)\(\approx5,13\left(\%\right)\)

b: Thay x=25 vào B, ta được:
\(B=\dfrac{5-3}{5+2}=\dfrac{2}{7}\)
thay x=25 vào biểu thức B ta có :
\(\dfrac{\sqrt{25}-3}{\sqrt{25}+2}\)=\(\dfrac{5-3}{5+2}\)=\(\dfrac{2}{7}\)
vậy tại x=25 thì B=\(\dfrac{2}{7}\)

Câu 2:
Ta có: \(x^3+3x^2-4x-12=0\)
\(\Leftrightarrow x^2\left(x+3\right)-4\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-2\right)\left(x+2\right)=0\)
hay \(x\in\left\{-3;2;-2\right\}\)

b: x1^2+m(x2)=13
=>x1^2+x2(x1+x2)=13
=>(x1+x2)^2-x1x2=13
=>m^2-m+1-13=0
=>m^2-m-12=0
=>m=4; m=-3

a: \(B=\dfrac{x+\sqrt{x}-1-x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{1}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
b: \(B-\dfrac{1}{3}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{3}\)
\(=\dfrac{3\sqrt{x}-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\left(\sqrt{x}+1\right)^2}{3\left(x+\sqrt{x}+1\right)}< 0\)
=>B<1/3

10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)
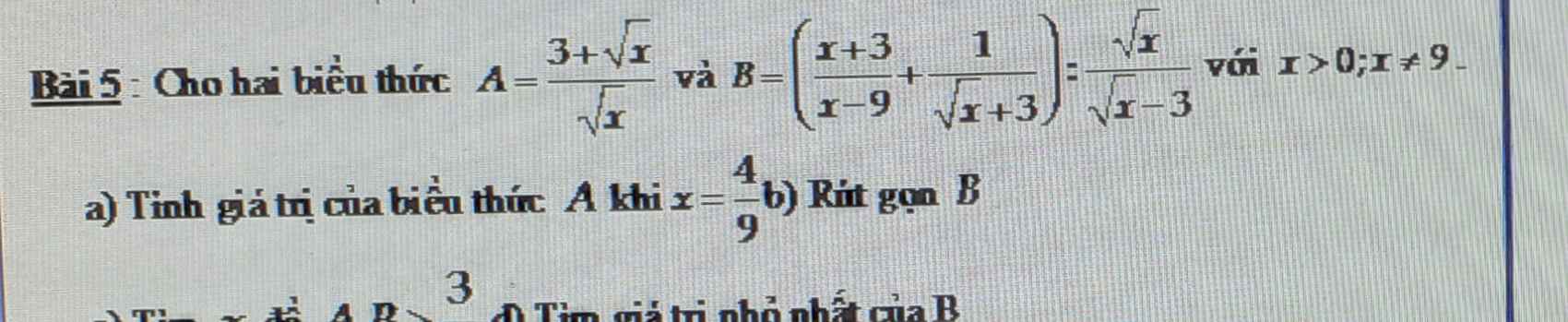




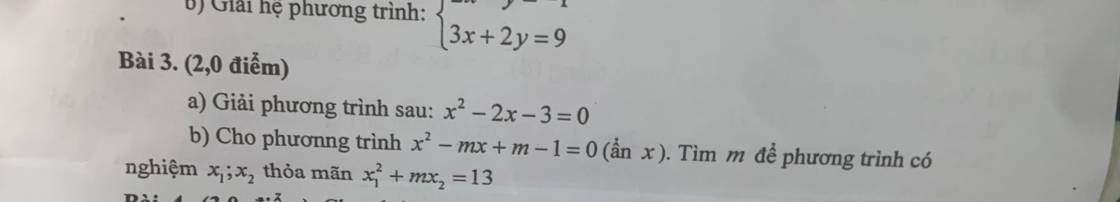
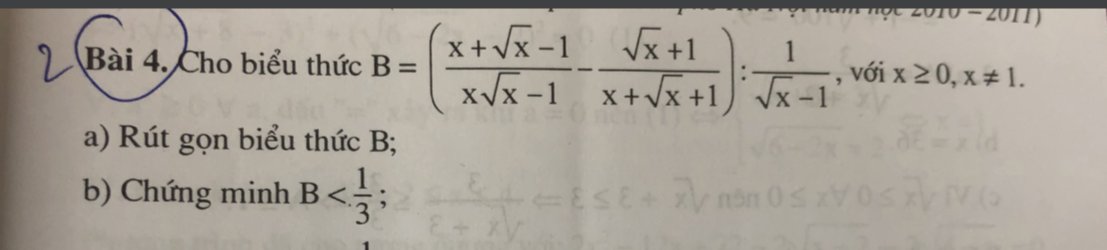
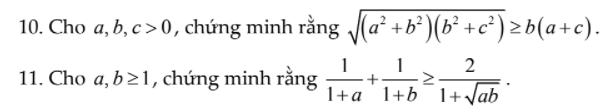 !
!