Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \({S_{ABCD}} = 4.{S_{AEB}}\) = 4. \(\frac{1}{2}.1.1\) = 2 (m2)
b) AB = \(\sqrt {S{}_{ABCD}} = \sqrt 2 \) (m)
a: AC=DB=2m
S ABCD=1/2*2*2=2m2
b: AB=căn 1^2+1^2=căn 2(m)

Bài 1 : A B C D 4
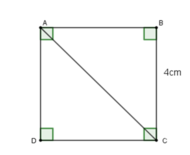
Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)
\(\Rightarrow AB=BC=CD=AD=4\)cm
Áp dụng định lí pytago tam giác ADC vuông tại D ta có :
\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm
Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm
Bài 2 :
A B C D 3 căn27
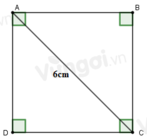
Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)
Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :
\(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm

O D A B C 1 2 1
Ta có: AD = BC = 3 (cm) (tính chất hình thang cân)
ˆABD=ˆBDC (so le trong)
ˆADB=ˆBDC(gt)
⇒ˆABD=ˆADB
⇒ ∆ ABD cân tại A
⇒ AB = AD = 3 (cm)
∆ BDC vuông tại B
⇒ˆBDC+ˆC=90độ ⇒BDC^+C^=90độ
ˆADC=ˆCADC^=C^ (gt)
Mà ˆBDC=12ˆADC nên ˆBDC=12ˆCBD
C^+12C^=90độ ⇒C^=60độ
Từ B kẻ đường thẳng song song AD cắt CD tại E.
Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE
⇒ DE = 3 (cm), BE = 3 (cm)
ˆBEC=ˆADC (đồng vị )
Suy ra: ˆBEC=ˆCBE
⇒ ∆ BEC cân tại B có C^=60 độ
⇒ ∆ BEC đều
⇒ EC = BC = 3 (cm)
CD = CE + ED = 3 + 3 = 6 (cm)
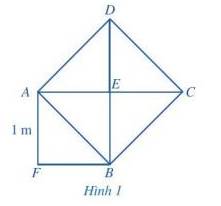



a: ABCD là hình vuông
=>AB=BC=CD=DA và \(\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{ADC}=90^0\) và AC là phân giác của \(\widehat{DAB}\) và DB là phân giác của góc ADC; BD là phân giác của góc ABC
AC là phân giác của góc DAB
=>\(\widehat{CAB}=\dfrac{1}{2}\widehat{DAB}=\dfrac{1}{2}\cdot90^0=45^0\)
AEBF là hình vuông
=>AB là phân giác của \(\widehat{FAE}\) và \(\widehat{FAE}=90^0\)
=>\(\widehat{BAE}=\dfrac{1}{2}\cdot\widehat{EAF}=45^0\)
\(\widehat{BAE}=45^0\)
\(\widehat{BAC}=45^0\)
Do đó: \(\widehat{BAE}=\widehat{BAC}=45^0\)
=>AE và AC là hai tia trùng nhau
=>A,E,C thẳng hàng
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
AEBF là hình vuông
=>BA là phân giác của góc EBF
=>\(\widehat{ABE}=\dfrac{1}{2}\cdot\widehat{FBE}=45^0\)
=>\(\widehat{ABE}=\widehat{ABD}\)
=>BE,BD là hai tia trùng nhau
=>B,E,D thẳng hàng
B,E,D thẳng hàng
A,E,C thẳng hàng
Do đó: BD cắt AC tại E
ADCB là hình vuông
=>AC=BD và AC vuông góc với BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại E và E là trung điểm chung của AC và DB
E là trung điểm của AC nên AC=2AE=2(cm)
E là trung điểm của BD nên BD=2EB=2(cm)
Xét tứ giác ADCB có DB\(\perp\)AC
nên \(S_{ADCB}=\dfrac{1}{2}\cdot DB\cdot AC=\dfrac{1}{2}\cdot2\cdot2=2\left(cm^2\right)\)
b: ADCB là hình vuông
=>\(S_{ADCB}=AB^2\)
=>\(AB^2=2\)
=>\(AB=\sqrt{2}\left(cm\right)\)