Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

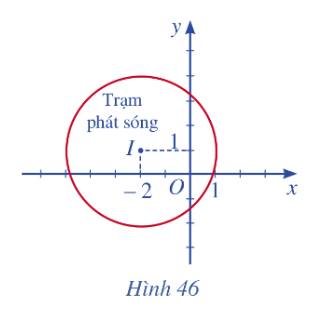
a) Phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
b) Khoảng cách từ tâm I đến A là: \(IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( {3 - 1} \right)}^2}} = \sqrt 5 \)
Do \(IA < 3\) nên điểm A nằm trong đường tròn ranh giới. Vậy nên người A có thể dịch vụ của trạm.
c) Khoảng cách từ tâm I đến B là: \(IB = \sqrt {{{\left( { - 3 + 2} \right)}^2} + {{\left( {4 - 1} \right)}^2}} = \sqrt {10} \)
Khoảng cách ngắn nhất theo đường chim bay để 1 người ở B di chuyển đến vùng phủ sóng là:
\(IB - R = \sqrt {10} - 3\left( {km} \right)\)

a) Tàu A di chuyển theo hướng vecto \(\overrightarrow {{u_1}} = \left( { - 35;25} \right)\)
Tàu B di chuyển theo hướng vecto \(\overrightarrow {{u_2}} = \left( { - 30; - 40} \right)\)
Gọi \(\alpha \) là góc giữa hai đường đi của hai tàu, ta có:
\(\cos \alpha = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {\left( { - 35} \right).\left( { - 30} \right) + 25.\left( { - 40} \right)} \right|}}{{\sqrt {{{\left( { - 35} \right)}^2} + {{25}^2}} .\sqrt {{{\left( { - 30} \right)}^2} + {{\left( { - 40} \right)}^2}} }} = \frac{1}{{5\sqrt {74} }}.\)
b) Sau t giờ, vị trí của tàu A là điểm M có tọa độ là: \(M\left( {3 - 35t; - 4 + 25t} \right)\)
Sau t giờ, vị trí của tàu B là điểm N có tọa độ là: \(N\left( {4 - 30t;3 - 40t} \right)\)
Do đó, \(\overrightarrow {MN} = \sqrt {{{\left( {1 + 5t} \right)}^2} + {{\left( {7 - 65t} \right)}^2}} = \sqrt {4250{t^2} - 900t + 50} = \sqrt {4250{{\left( {t - \frac{9}{{85}}} \right)}^2} + \frac{{40}}{{17}}} \ge \sqrt {\frac{{40}}{{17}}} \approx 1,53\left( {km} \right)\)
Suy ra MN nhỏ nhất xấp xỉ 1,53km khi \(t = \frac{9}{{85}}\)
Vậy sau \(\frac{9}{{85}}\) giờ kể từ thời điểm xuất phát thì hai tàu gần nhau nhất và cách nhau 1,53km
c) Vị trí ban đầu của tàu A tại \({M_o}\) ứng với \(t = 0\) , khi đó \({M_o}\left( {3; - 4} \right)\)
Tàu B di chuyển theo đường thẳng có vecto pháp tuyến \(\overrightarrow n = \left( {40; - 30} \right)\) và đi qua điểm \(K\left( {4;3} \right)\) Phương trình tổng quát của là: \(40\left( {x - 4} \right) - 30\left( {y - 3} \right) = 0 \Leftrightarrow 4x - 3y - 7 = 0\) \(\Delta \)
Ta có: \(d\left( {{M_o},\Delta } \right) = \frac{{\left| {4.3 - 3.\left( { - 4} \right) - 7} \right|}}{{\sqrt {{4^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{17}}{5} = 3,4\left( {km} \right)\)
Vậy nếu tàu A đứng yên ở vị trí ban đầu còn tàu B di chuyển thì khoảng cách ngắn nhất giữa hai tàu bằng 3,4km.

a) Vị trí máy bay vào lúc 14 giờ 30 phút là: \(\left\{ \begin{array}{l}x = \frac{{1600}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 300\\y = \frac{{1900}}{3} - \frac{{1400}}{3}.\frac{1}{2} = 400\end{array} \right.\)
Vậy tọa độ máy bay là \(\left( {300;400} \right)\). Thời điểm này máy bay đã xuất hiện trên màn hình ra đa.
b) Ta có: \(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} \).
Do có \(M{O_{\min }} = 50\sqrt 2 \Leftrightarrow t = \frac{5}{4}\).
Vậy sau khi bay \(\frac{5}{4} = 1,25\) (giờ) tức là lúc 15h15p thì máy bay gần ra đa nhất và khoảng cách từ ra đa đến máy bay khi đó là \(50\sqrt 2 \left( {km} \right)\).
c) Máy bay rời khỏi màn hình ra đa khi mà khoảng cách từ M đến O lớn hơn 500km tức là:
\(MO = \sqrt {{{\left( {\frac{{1600}}{3} - \frac{{1400}}{3}t} \right)}^2} + {{\left( {\frac{{1900}}{3} - \frac{{1400}}{3}t} \right)}^2}} \ge 500 \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{2}\\t = 2\end{array} \right.\)
Vậy sau khi bay được 2h tức là lúc 16h thì máy bay thoát khỏi màn hình ra đa.

vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv⚽☺


Gọi M (x; y) là vị trí của tâm bão tại thời điểm t giờ.
Tâm bão chuyển động đều từ A (13,8; 108,3) đến B (14,1;106,3).
Khi đó ta có: \(\overrightarrow {AM} = \frac{t}{{12}}.\overrightarrow {AB} \)
\(\begin{array}{l} \Leftrightarrow (x - 13,8;y - 108,3) = \frac{t}{{12}}.(14,1 - 13,8;106,3 - 108,3)\\ \Leftrightarrow (x - 13,8;y - 108,3) = \frac{t}{{12}}.(0,3; - 2)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 13,8 = \frac{t}{{40}}\\y - 108,3 = - \frac{t}{6}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13,8 + \frac{t}{{40}}\\y = 108,3 - \frac{t}{6}\end{array} \right.\end{array}\)
Vậy tại thời điểm t giờ, tâm bão ở vị trí \(M\left( {13,8 - \frac{t}{{40}};108,3 - \frac{t}{6}} \right)\)

Khi tới vị trị M(3;4), vật bị văng khỏi quỹ đạo tròn và ngay sau đó bay theo hướng tiếp tuyến d của đường tròn tại điểm M. Do đó, d đi qua điểm M và nhận vecto \(\overrightarrow {OM} = \left( {3;4} \right)\) làm vecto pháp tuyến. Vậy phương trình của d là: \(3\left( {x - 3} \right) + 4\left( {y - 4} \right) = 0 \Leftrightarrow 3x + 4y - 25 = 0\).

Gọi J là vị trí âm thanh phát đi. Ta có J cách đều O, A, B. Do đó J là giao của hài đường trun trực \({d_1},{d_2}\) tương ứng của OA, OB. Đường thẳng \({d_1}\) đi qua trung điểm M của OA và vuông góc với OA. Ta có \(M\left( {\frac{1}{2};0} \right)\) và \(\overrightarrow {{n_{{d_1}}}} = \overrightarrow {OA} = \left( {1;0} \right)\).
Phương trình đường thẳng \({d_1}\) là \(1\left( {x - \frac{1}{2}} \right) + 0\left( {y - 0} \right) = 0 \Leftrightarrow x = \frac{1}{2}\).
Tương tự, phương trình đường thẳng \({d_2}\) là \(x + 3y - 5 = 0\).
Tọa độ điểm J là nghiệm của hệ \(\left\{ \begin{array}{l}x = \frac{1}{2}\\x + 3y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{3}{2}\end{array} \right.\).
Vậy \(J\left( {\frac{1}{2};\frac{3}{2}} \right)\).

a) Ta có: \(\overrightarrow {BC} = \left( { - 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right)\)
\(\cos \widehat {ABC} = \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \frac{{\left( { - 7} \right).3 + 1.3}}{{\sqrt {{{\left( { - 7} \right)}^2} + {1^2}} .\sqrt {{3^2} + {3^2}} }} = - \frac{3}{5} \Rightarrow \widehat {ABC} \approx {126^o}\)
b) Ta có: \(\overrightarrow {BC} = \left( { - 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right),\overrightarrow {AC} = \left( { - 10; - 2} \right)\)
Suy ra: \(\begin{array}{l}AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \\AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt {104} \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{{\left( { - 7} \right)}^2} + {1^2}} = \sqrt {50} \end{array}\)
Vậy chu vi tam giác ABC là: \({P_{ABC}} = 2\sqrt {26} + 8\sqrt 2 \)
c) Để diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM thì M phải là trung điểm BC.
Vậy tọa độ điểm M là: \(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = \frac{{ - 9}}{2}\\\frac{{{y_B} + {y_C}}}{2} = \frac{3}{2}\end{array} \right.\). Vậy \(M\left( {\frac{{ - 9}}{2};\frac{3}{2}} \right)\)

Gọi B(x; y) là vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Do tàu khởi hành từ A đi chuyển với vận tốc được biểu thị bởi vectơ \(\overrightarrow v = \left( {3;4} \right)\) nên cứ sau mỗi giờ, tàu đi chuyển được một quãng bằng \(\left| {\overrightarrow v } \right|\).
Vậy sau 1,5 giờ tàu di chuyển tới B, ta được: \(\overrightarrow {AB} = 1,5.\overrightarrow v \)
\(\begin{array}{l} \Leftrightarrow (x - 1;y - 2) = 1,5\;.\left( {3;4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 4,5\\y - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5,5\\y = 8\end{array} \right.\end{array}\)
Vậy sau 1,5 tàu ở vị trí (trên mặt phẳng tọa độ) là B(5,5; 8).

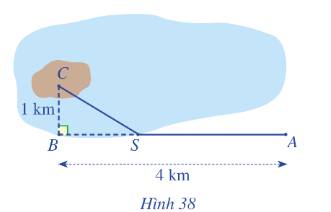
Gọi khoảng cách từ A đến S là x (km) (0<x<4)
\( \Rightarrow BS = 4 - x\)(km)
\( \Rightarrow CS = \sqrt {C{B^2} + B{S^2}} \)\( = \sqrt {1 + \left( {4 - {x^2}} \right)} \)(km)
Tổng số tiền từ A đến C là:
\(3.SA + 5.SC = 3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} \)(triệu đồng)
Khi đó ta có phương trình:
\(3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16\)
\( \Leftrightarrow 5\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16 - 3x\)
\(\begin{array}{l}25.\left( {{x^2} - 8x + 17} \right) = {\left( {16 - 3x} \right)^2}\\ \Leftrightarrow 25{x^2} - 200x + 425 = 256 - 96x + 9{x^2}\\ \Leftrightarrow 16{x^2} - 104x + 169 = 0\\ \Leftrightarrow x = \frac{{13}}{4}\left( {tm} \right)\end{array}\)
Do \(16 - 3x > 0 \Leftrightarrow \forall 0 < x < 4\)
=> \(SC = \sqrt {1 + \left( {4 - {x^2}} \right)} = 1,25\)
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)