Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có EO//DC ⇒ OE/DC = AO/AC (1)
OF//DC ⇒ OF/DC = BO/BD (2)
Ta có: AB//DC ⇒ OA/OC = OB/OD
⇒ OA/ (OC + OA) = OB/(OD+ OB) ⇒ OA/AC = OB/BD (3)
Từ (1),(2),(3) ta có OE/DC = OF/DC ⇒ OE = OF
Ta có AB//EF
⇒ AN/EO = KN/KO và BN/FO = KM/KO
⇒ AN/EO = BN/FO ⇒ AN = BN
Tương tự: FE//DC ⇒ EO/DM = KO/KM
và FO/CM = KO/KM ⇒EO/DM=FO/CM ⇒ DM=CM

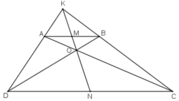
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒ 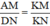 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒ 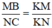 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
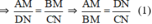
ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒ 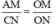 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒ 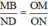 (Hệ quả định lý Ta-let)
(Hệ quả định lý Ta-let)
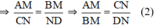
Từ (1) và (2) suy ra 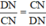 ⇒ CN = DN ⇒ AM = MB
⇒ CN = DN ⇒ AM = MB
Vậy M, N là trung điểm AB, CD.

A B C D N K M O
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒ \(\frac{AM}{DN}=\frac{KM}{KN}\)( hệ quả của định lí Talet )
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒ \(\frac{MB}{NC}=\frac{KM}{KN}\)( hệ quả của định lí Talet )
\(\Rightarrow\frac{AM}{DN}=\frac{BM}{CN}\Rightarrow\frac{AM}{BM}=\frac{DN}{CN}\left(1\right)\)
.ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒ \(\frac{AM}{CN}=\frac{ON}{CN}\)( hệ quả của định lí Talet )
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒ \(\frac{MB}{ND}=\frac{OM}{ON}\)( hệ quả của định lí Talet )
\(\Rightarrow\frac{AM}{CN}=\frac{BM}{ND}\Rightarrow\frac{AM}{BM}=\frac{CN}{DN}\left(2\right)\)
Từ (1)(2) , suy ra :
\(\frac{DN}{CN}=\frac{CN}{DN}\Rightarrow CN=DN\Rightarrow AM=MB\)
Vậy M, N là trung điểm AB, CD.

Câu hỏi của Lưu Đức Mạnh - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài giải tại đây nhé.

Vì OE // DC ==> OA/AC = OE/DC (định lý Ta-let) (1)
Vì OF // DC ==> OB/BD = OF/DC (định lý Ta-let) (2)
Vì AB // CD ==> OA/OC = OB/OD (định lý ta-let)
Theo tính chất dãy tỉ số bằng nhau ta có:
OA/OC = OB/OD <=> OA / (OA + OC) = OB / (OB + OD)
<=> OA / AC = OB / BD (3)
Từ (1), (2) và (3) suy ra ta có:
OE / DC = OF / DC <=> OE = OF (đpcm)

1.
O A B D C E
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB