Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ai k mình mình k lại
Ta có : \(S^{AID}=S^{BIC}\)
Mà theo đề ra : \(S^{CID}-S^{AIB}=193cm^2\)
\(\Rightarrow\left(S^{AID}+S^{CID}\right)-\left(S^{BIC}+S^{AIB}\right)=193cm^2\)
\(\Rightarrow S^{ADC}-S^{ABC}=193cm^2\)
Do \(\frac{AB}{CD}=\frac{2}{3}\Rightarrow\frac{S^{ABC}}{S^{ADC}}=\frac{2}{3}\)
\(\Rightarrow S^{ABCD}=S^{ADC}+S^{ABC}=193:\left(3-2\right)x\left(3+2\right)=965cm^2\)
Đ/S : ... ...
Hình thang ABCD cho ta SAID=SBIC gọi diện tích 2 hình tam giác này là n.
Xét 2 tam giác AIB và AID chung đường cao kẻ từ A nên 2 cạnh đáy IB và ID tỉ lệ với 2 diện tích: IB/ID = 24,5/n
Tương tự với 2 tam giác CIB và CID ta có IB/ID = n/98
Suy ra: 24,5/n = n/98
n x n = 98 x 24,5 = 2401
Vậy n= 49
SABCD = 24,5 + 98 + 49x2 = 220,5 (cm2)
tk nha bạn
thank you bạn
(^_^)
SIAD = SIBC = 193 : 2 x 3 = 289,5 ( cm2 )
SICD = 289,5 : 2 x 3 = 434,25 ( cm2 )
=> SABCD = 434,25 + 289,5 + 289,5 + 193 = 1206,25 ( cm2 )
Chúc bạn may mắn!
Câu hỏi của Sóc Lá Cây - Toán lớp 5 - Học toán với OnlineMath
Tui làm đó nha
Đúng 100%
Đúng 100%
Đúng 100%
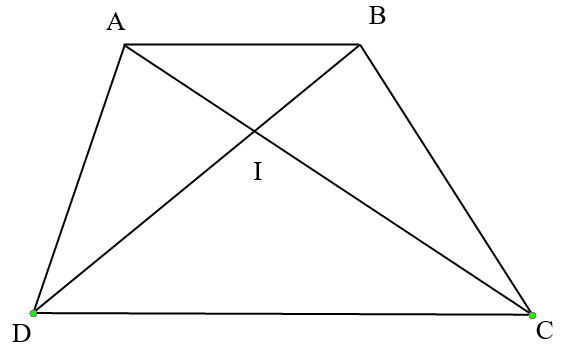
Bài giải chi tiết:
Ta có: SBDC = 3/2 SABC (cùng chiều cao hạ từ C và AB = 2/3 CD)
Từ đó ta có: SBIC + SCID = 3/2 (SBIC + SAIB)
Ta lại có: SCID = SAIB + 193
Suy ra: SBIC + SAIB + 193 = SBIC + SAIB
Hay: SAIB + SBIC = 386 (cm2)
Vậy: SABC = SAIB + SBIC = 386 (cm2)
Ta lại có: SACD = SBCD do hai tam giác này có cùng chiều cao là chiều cao hình thang ABCD và có chung tam giác CID. Suy ra: SAID = SBIC
Từ đó ta có: SACD = SABC + 193 = 579 (cm2)
Vậy: SABCD = SABC + SACD = 386 + 579 = 965 (cm2)