Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình không biết vẽ hình trên đây bạn tự vẽ hình nhé
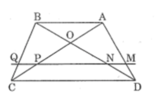
a, Vì MN//AB=>MN//AB//CD(vì AB//CD)
PQ//DC=>PQ//DC//AB(vì AB//CD)
=>MN//PQ
Xét hình thang ABQP có: AM=PM(M là trung điểm của AB)
MN//PQ//AB
=>BN=NQ hay N là trung điểm của BQ(1)
Xét hình thang MNCD có: MP=DP(P là trung điểm của MD)
MN//PQ//CD
=>NQ=QC hay Q là trung điểm của NC(2)
Từ (1) và (2)=>BN=NQ=QC
b,Xét hình thang ABQP có: AM=PM(M là trung điểm của AP)
BN=QN(N là trung điểm của BQ)
=>MN là đường trung bình của hình thang ABQP
=>MN=\(\frac{AB+PQ}{2}\)
=>AB+PQ=2MN
c, Xét hình thang MNCD có: MP=DP(P là trung điểm của MD)
NQ=CQ(Q là trung điểm của NC)
=>PQ là đường trung bình của hình thang MNCD
=>PQ=\(\frac{MN+CD}{2}\)
=>MN+CD=2PQ
d, Vì AB+PQ=2MN =>AB=2MN-PQ(3)
MN+DC=2PQ =>DC=-MN+2PQ(4)
Cộng từng vế tương ứng của (3) và (4) ta được:
AB+CD=2MN-PQ+(-MN)+2PQ
AB+CD=MN+PQ

A B C D E M P F N Q 8cm 12cm
Theo giả thiết ta có:
AE = EM = MP = PD => AE + EM = MP+PD
C/ m tương tự ta có: BF +FN = NQ + QC
=> MN là đg TB hình thang ABCD
\(\Rightarrow MN=\frac{AB+CD}{2}=\frac{8+12}{2}=10\left(cm\right)\)
C/m tương tự ta có:
\(EF=\frac{AB+MN}{2}=\frac{8+10}{2}=9\left(cm\right)\)
\(PQ=\frac{MN+CD}{2}=\frac{10+12}{2}=11\left(cm\right)\)
Vậy...

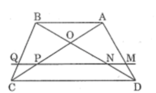
Trong ΔADB, ta có: MN // AB (gt)
Suy ra: ![]() hệ quả định lí ta-lét) (1)
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: 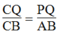 Hệ quá định lí Ta-lét) (2)
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: ![]() (Định lí Ta-lét) (3)
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra ![]() hay MN = PQ.
hay MN = PQ.

Trong ΔADB, ta có: MN // AB (gt)
Suy ra: ![]() hệ quả định lí ta-lét) (1)
hệ quả định lí ta-lét) (1)
Trong ΔACB, ta có: PQ // AB (gt)
Suy ra: 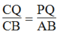 Hệ quá định lí Ta-lét) (2)
Hệ quá định lí Ta-lét) (2)
Lại có: NQ // AB (gt)
AB // CD (gt)
Suy ra: NQ // CD
Trong ΔBDC, ta có: NQ // CD (chứng minh trên)
Suy ra: 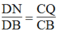 (Định lí Ta-lét) (3)
(Định lí Ta-lét) (3)
Từ (1), (2) và (3) suy ra 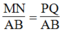 hay MN = PQ.
hay MN = PQ.