Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔADC có MI//DC
nên \(\dfrac{MI}{DC}=\dfrac{AM}{AD}=\dfrac{1}{2}\)
=>\(\dfrac{MI}{12}=\dfrac{1}{2}\)
=>\(MI=6\left(cm\right)\)
Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét hình thang ABCD có
M,N lần lượt là trung điểm của AD,BC
=>MN là đường trung bình của hình thang ABCD
=>\(MN=\dfrac{AB+CD}{2}=\dfrac{6+12}{2}=\dfrac{18}{2}=9\left(cm\right)\)

a/
△ACD có:
- MN lần lượt đi qua trung điểm của AD và AC tại M và N
=> MN là đường trung bình của △ACD
Mặt khác, hình thang ABCD có:
- MP lần lượt đi qua trung điểm của AD và BC tại M và P
=> MP là đường trung bình của hình thang ABCD
=> MN trùng MP
Vậy: M, N, P thẳng hàng. (đpcm)
b/
- MN là đường trung bình của △ACD (cmt)
=> \(MN=\dfrac{1}{2}CD\)
Hay: \(MN=\dfrac{1}{2}.7=3,5\left(cm\right)\)
- MP là đường trung bình của hình thang ABCD (cmt)
=> \(MP=\dfrac{1}{2}AB.CD\)
Hay: \(MP=\dfrac{5+7}{2}=6\left(cm\right)\)
- \(NP=MP-MN\)
Hay: \(NP=6-3,5=2,5\left(cm\right)\)
- Nhận xét: Độ dài MP = 1/2 tổng độ dài hai đáy AB và CD
Vậy:
\(MN=3,5\left(cm\right)\)
\(NP=2,5\left(cm\right)\)
\(MP=6\left(cm\right)\)

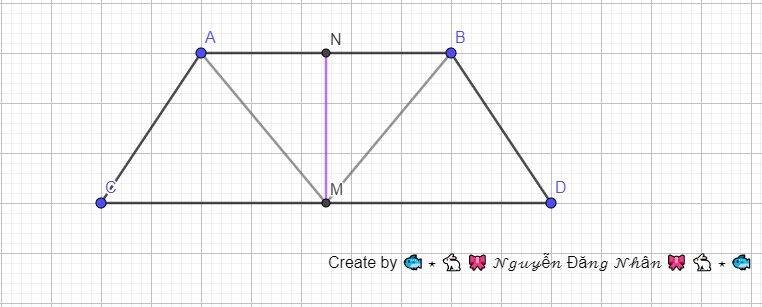
a) Xét 2 tam giác AMC và BMD có:
\(\widehat{C}=\widehat{D}\) (góc kề một đáy)
\(AC=BD\) (cạnh bên)
\(MC=MD\) (giả thiết)
\(\Rightarrow\Delta AMC=\Delta BMC\) (cạnh.góc.cạnh)
\(\Rightarrow AM=BM\)
b) Xét 2 tam giác NMA và NMB có:
\(NA=NB\) (giả thiết)
\(NM\): cạnh chung
\(MA=MB\) (chứng minh trên)
\(\Rightarrow\Delta NMA=\Delta NMB\)
\(\Rightarrow\widehat{MNA}=\widehat{MNB}\)
Mà 2 góc \(\widehat{MNA}=\widehat{MNB}\) là 2 góc kề bù, nên:
\(\widehat{MNA}=\widehat{MNB}=\dfrac{180^o}{2}=90^o\)
Vậy MN là đường cao:

a: Xét ΔADM và ΔBCM có
AD=BC
góc ADM=góc BCM
DM=CM
=>ΔADM=ΔBCM
=>MA=MB
b: ΔMAB cân tại M
mà MN là đường trung tuyến
nên MN vuông góc AB

1.
Độ dài đường trung bình của hình thang là:
$\frac{AB+CD}{2}=\frac{4+12}{2}=8$ (cm)
2. $M\in BC$ và $MB=MC$ nên $M$ là trung điểm của $BC$
Tam giác $ABC$ vuông tại $A$ có đường trung tuyến $AM$ ứng với cạnh huyền nên $MA=\frac{BC}{2}=\frac{7}{2}$ (cm)
1: Độ dài đường trung bình của hình thang ABCD(AB//CD) là:
\(\dfrac{AB+CD}{2}=\dfrac{4+12}{2}=\dfrac{16}{2}=8\left(cm\right)\)
2: Ta có: MB=MC(Gt)
mà M nằm giữa hai điểm B và C(gt)
nên M là trung điểm của BC
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
\(\Leftrightarrow AM=\dfrac{7}{2}=3.5\left(cm\right)\)
Vậy: AM=3,5cm

Vì MN là đường trung bình của hình thang ABCD nên:
MN=(AB+CD)/2
=>MN=(8+12)/2
=>MN=20/2
=>MN=10 cm.
#Hok tốt~~~