Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hình thang ABCD (AB song song CD) có AB=10, BD=6, MN= 4 (M,N là trung điểm AB,CD). Tính \(S_{ABCD}\)


Bài 2: Từ A kẻ H, từ B kẻ K
Suy ra: AB=HK=10cm
=> BH=KC=\(\frac{26-10}{2}=8\)cm
=> BH=8 và HC= 10+8=18
=> AH2= HB.HC=8.18 <=>AH= 12
=> S= \(\frac{10+26}{2}.12=216\) cm2
Bài 1: \(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Leftrightarrow BC=\sqrt{5^2+12^2}=13\)
Suy ra: BM=MC=BC/2=6,5
\(\Rightarrow MN^2=NC^2-MC^2\) (Tam giác MNC vuông tại M)
\(\Leftrightarrow MN=\sqrt{12^2-6,5^2}=\frac{\sqrt{407}}{2}\)

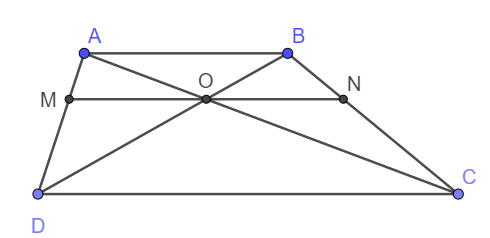
a) Do AB//CD nên áp dụng hệ quả định lý Ta let ta có:
\(\frac{AO}{OC}=\frac{OB}{OD}\) hay \(\frac{DO}{DB}=\frac{OC}{AC}\)
Xét tam giác ABD có OM//AB nên \(\frac{OM}{AB}=\frac{DO}{DB}\)
Tương tự \(\frac{ON}{AB}=\frac{CO}{CA}\)
Vậy nên \(\frac{OM}{AB}=\frac{ON}{AB}\Rightarrow OM=ON\)
b) Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OM=ON=\frac{k}{k+1}\Rightarrow MN=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{MN}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
c) Ta thấy ngay \(\Delta COD\sim\Delta AOB\left(g-g\right)\) theo tỉ lệ k ở câu b.
Vậy thì \(\frac{S_{COD}}{S_{AOB}}=\frac{2009^2}{2008^2}=\left(\frac{2009}{2008}\right)^2=k^2\Rightarrow k=\frac{2009}{2008}\)
Từ đó ta có \(\frac{OC}{OA}=\frac{DO}{OB}=\frac{2009}{2008}\)
Vậy thì \(\frac{S_{ADO}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{ADO}=\frac{2009}{2008}.2008^2=2009.2008\)
\(\frac{S_{BOC}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{BOC}=\frac{2009}{2008}.2008^2=2009.2008\)
Suy ra \(S_{ABCD}=S_{AOB}+S_{DOC}+S_{AOD}+S_{BOC}=2008^2+2009^2+2.2008.2009\)
\(=\left(2008+2009\right)^2=4017^2\left(cm^2\right)\)

A B C D O N M P
+) Ta có: DP // AB => ^APD = ^BAP (2 góc so le trong). Mà ^BAP = ^NMB (Do MN // AP)
Nên ^APD = ^NMB => \(\Delta\)ADP ~ \(\Delta\)NBM (g.g) => \(\frac{AD}{NB}=\frac{DP}{BM}\)=> \(AD.BM=NB.DP\)
Hoặc \(AB.BM=NB.DP\)=> \(OB^2=NB.DP\)(Do \(AB.BM=\frac{AB^2}{2}=OB^2\)theo ĐL Pytago)
Hay \(OB.OD=NB.DP\)=> \(\frac{OB}{DP}=\frac{NB}{OD}\)
Xét \(\Delta\)BNO và \(\Delta\)DOP có: ^OBN = ^PDO (=450) \(\frac{OB}{PD}=\frac{NB}{OD}\)(cmt)
=> \(\Delta\)BNO ~ \(\Delta\)DOP (c.g.c) (đpcm).
+) \(\Delta\)BNO ~ \(\Delta\)DOP (cmt) => ^BON = ^DPO (1)
Trong \(\Delta\)ODP có: ^DOP + ^DPO = 1800 - ^ODP = 1350 (2)
Từ (1) và (2) suy ra ^DOP + ^BON = 1350 => ^NOP = 1800 - (^DOP + ^BON) = 450
Vậy ^NOP = 450.